On Attention Redundancy: A Comprehensive Study 论文笔记

论文主要信息

• 标题：On Attention Redundancy: A Comprehensive Study
• 作者：Yuchen Bian, Jiaji Huang, Xingyu Cai, Jiahong Yuan, and Kenneth Church.
• 机构：Baidu Research, Sunnyvale, CA, USA
• 来源：NAACL2019
• 代码：

摘要 Abstract

多层多头自注意机制在现代神经语言模型中得到了广泛的应用。注意头之间存在注意冗余现象，但文献中尚未对其进行深入研究。

本文以BERT-base模型为例，对注意冗余进行了全面的研究，为模型解释和模型压缩提供了依据。我们用5个W和How分析注意冗余。

1. (What)我们定义和重点研究从预训练和微调的BERT-base模型生成的冗余矩阵GLUE数据集。
2. (How)我们使用基于标记和基于句子的距离函数来度量冗余。
3. (Where)注意头之间存在明显且相似的冗余模式(聚类结构)。
4. (When)在训练前和微调阶段，冗余模式是相似的。
5. (Who)我们发现冗余模式与任务无关。类似的冗余模式甚至存在于随机生成的标记序列。
6. (“Why”)我们还评估了训练前dropout率对注意力冗余的影响。

基于阶段无关和任务无关的注意冗余模式，我们提出了一种简单的zero-shot剪枝方法作为案例研究。通过对GLUE任务进行微调的实验验证了该方法的有效性。对注意力冗余度的综合分析使得模型理解和zero-shot模型修剪成为可能。

9 结论 Conclusion

我们以BERT-base模型为例，全面研究了基于多层多头自注意的语言模型中的注意冗余问题。

通过词符级和句子级的距离函数测量冗余度，在这两个层次上，我们发现许多头彼此之间没有区别，并且观察到明显的聚类效应。

我们发现注意冗余是阶段独立和任务无关的。具体来说，与预先训练的模型相比，在对多个下游任务进行微调后，冗余模式不会发生太大变化。我们也显示了隐藏转换和自我注意对冗余dropout率的复杂影响。

基于这些发现，我们设计了一个zero-shot策略来剪枝注意力头。与现有方法相比，zero-shot剪枝具有简单和鲁棒性(任务不可知)的特点。

1 导言 Introduction

注意力头存在冗余的情况。图1显示了平均超过1000个随机抽样句子的144 × 144对注意矩阵之间的冗余(距离)。我们可以在连续的注意层中看到清晰的冗余模式(距离区域较小的集群)。

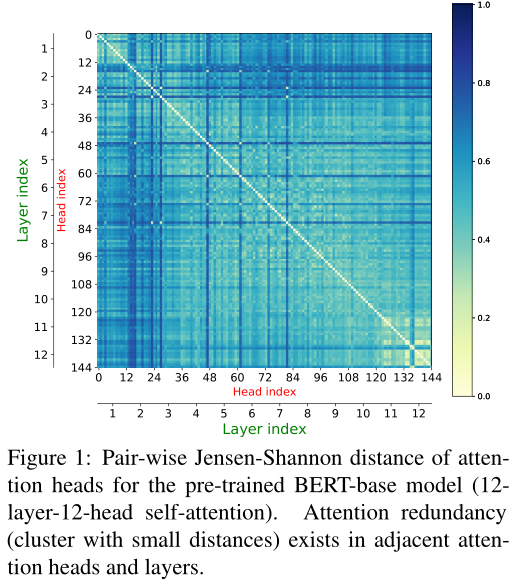
预训练BERT-base模型(12 - layer-12-head self-attention)的两两Jensen-Shannon距离。在相邻的注意头和注意层中存在着注意冗余(小距离聚类)。

对注意冗余度的分析有助于解释多层多头自注意体系结构。目前有一定的研究结果。虽然发现了冗余现象，但目前还没有研究对注意冗余模式本身(即图1中的144×144距离矩阵)进行深入的研究。这促使我们对注意冗余现象进行全面、互补的研究。

贡献

本文以BERT-base模型为代表模型，分析了具有五个w和How的注意冗余度。据我们所知，以下许多发现对研究界来说都是新的。

1. What 什么是注意力冗余?

给定一个距离函数，我们定义BERT-base模型的12 × 12注意矩阵的成对距离矩阵(∈R144×144)为注意冗余矩阵。本文以GLUE任务为研究对象，分别从预训练和精调的BERT-base模型中获取冗余矩阵。

1. How 如何衡量注意力冗余?

除了文献中使用的两种基于令牌的度量，即Jensen-Shannon距离(Clark等人，2019)和余弦相似度(Kovaleva等人，2019)，我们又使用了两个基于令牌的距离函数和三个基于句子的函数来测量注意冗余度，并分析了它们相似的冗余模式(详见4.1节)。其目的是为了减轻仅使用一个距离函数的测量偏差。基于句子的距离直接测量两个注意矩阵之间的关系，而不需要对标记进行平均。我们使用不同的距离函数来可视化冗余模式。

1. Where 注意力冗余存在于哪里?

我们分别在基于标记的冗余矩阵集合和基于句子的冗余矩阵集合中发现了共同的层次聚类结构。在冗余矩阵中，早期、中期和更深层注意层的注意头明显聚集在一起。我们还证明了在基于不同类型的距离生成的冗余矩阵中存在高度相关的相似冗余模式。

1. When 什么时候出现注意力冗余?

冗余是阶段无关的。在预训练阶段和微调阶段都发现了常见的冗余模式。对于具有任何距离函数的下游任务，我们注意到两个阶段之间高度相关的注意冗余模式。

1. Who 谁(哪个任务)有注意力冗余?

我们惊奇地发现冗余是与任务无关的。冗余模式在不同的任务之间高度相关。我们甚至在预训练的BERT-base模型中随机生成标记序列作为输入。非常相似的注意冗余模式也会出现。

基于这一惊人的发现，作为一个案例研究应用，我们提出了一种基于冗余矩阵聚类结果的简单的零镜头头部剪枝策略。与其他复杂的剪枝策略相比，例如，(Tang et al.， 2019;焦等，2019;Fan et al.， 2019;Wang et al.， 2019;McCarley, 2019)，最重要的是，在不知道微调任务的任何数据的情况下，这种修剪可以有效和高效地进行，仅仅基于一些随机生成的token序列与预先训练的BERT-base模型。唯一的努力是计算一个或几个冗余矩阵。结果表明，对于大多数GLUE任务，基于冗余矩阵的剪枝策略可以剪枝75% - 85%的注意力头，同时保持相当的微调性能。

1. Why “为什么”阶段独立和任务不可知的注意力冗余会发生?

很难说出冗余模式的原因(这就是为什么我们使用引号中的“为什么”)。然而，我们进行了实验来评估在训练前阶段dropout比率对注意冗余的影响，这被怀疑是原因之一(Clark et al.， 2019)。

当我们使用基于句子的距离时，会发现一种单调的趋势。当dropout率增加时，注意力集中就显得多余了。当我们使用基于标记的距离时，存在一个复杂的“N”形状效果。我们还注意到，冗余对隐藏线性转换中的漏出比对自我注意机制中的漏出更敏感。

我们认为，本文的这些新发现使得冗余分析在模型解释、模型压缩等方面具有广阔的研究前景。

2 相关工作 Related Work

现有文献从词/标记嵌入潜在空间、语言知识可解释性、注意机制等不同方面分析了基于语言模型(如BERT)的多层多头自我注意架构(Rogers等，2020)。

BERT注意层的输出是令牌嵌入向量。一个标记的一个输出向量聚合了整个句子的上下文信息。

另一组作品关注的是提取语言知识的能力。BERT可以获得句法依赖关系、词性标记、单词消歧等(Ethayarajh, 2019;Vig和Belinkov, 2019年;Clark et al.， 2019;戈德堡,2019)。这表明同一层学习类似的知识(Clark et al.， 2019)。

由于自我注意是BERT的基本机制，现有的研究也对注意力向量和矩阵的提取进行了研究。这些与我们的研究最相关。Clark等人(2019)和Kovaleva等人(2019)发现了一些常见的注意模式，如分隔符标记、块和异构模式的模式。此外，在注意头中也发现了冗余和过度参数化。通过使用基于注意的探测分类器，Clark等人(2019)发现，同一层的头部通常会表现出类似的行为。注意头可以用不同的策略进行修剪，但在下游任务中保持可比较的表现。有些层甚至可以减少到一个头部(Michel等人，2019年)。

理解注意力冗余可以帮助解释经过训练/微调的语言模型，并指导模型压缩。但目前还没有关于注意冗余的系统研究。本文对注意力冗余进行了深入的研究。

3 What: 冗余矩阵 What: Redundancy Matrices

本文以BERT-base模型为代表，研究了多层多头自注意机制中存在的注意冗余问题。BERT模型作为一种预训练的语言模型，在许多下游的语言理解任务中具有良好的调优性能。

BERT-base模型有12个自我注意层，每个层由12个自我注意头组成。对于一个输入(带有特殊标记[CLS]和[SEP]的句子或句子对)，我们提取12 × 12的注意力矩阵。每个矩阵的大小为n × n，其中n为BERT标记化后的标记数。给定一个度量(例如，距离函数)和提取的注意力矩阵，我们可以测量每一对144个注意力矩阵之间的关系，例如图1中的144 × 144矩阵。我们将144个正面(即注意力矩阵)之间的成对关系定义为冗余矩阵。我们认为，注意头之间的距离越小，注意冗余度就越大。

实验介绍

对于研究对象，我们使用了著名的自然语言理解基准GLUE task (Wang et al.， 2018)作为注意力冗余分析的评价对象。在GLUE中，CoLA是用于英语句子可接受性判断的。SST-2和STS-B是情绪分析任务。MRPC和QQP用于句子对相似度分类。MNLI QNLI,RTE是自然语言推理任务。CoLA和SST-2是单句任务，而其他人则预测一对句子之间的关系。除了STS-B是一个回归任务外，在BERT框架中，其他的都形成了分类任务。

在实验中，我们从每个开发集中随机选择1000个数据样本作为数据实例，并报告平均结果。我们将它们输入(预先训练和微调的)BERT-base模型，生成注意力矩阵。我们使用PyTorch BERT-base模型作为预训练模型3 (Wolf et al.， 2019)。为了进行精细调优，我们用建议的超参数max-length=128, num-epoch=3, batchsize-per-GPU=32在8个gpu上训练每个任务。本文的所有结果均为5次试验的平均值。

4 How:距离函数 How: Distance Functions

注意冗余的一个基本问题是如何度量两个注意矩阵之间的相似性或距离。距离越小，冗余越多。在本节中，我们将介绍两种距离函数，基于标记的距离和基于句子的距离。目的是检验它们在量化注意冗余时的可解释性和一致性，并缓解仅使用某一距离函数的测量偏差。

设$dist(Ai, Aj)$是一个距离函数，用来度量第$i$个和第$j$个注意矩阵$Ai$和$Aj$之间的关系。注意，我们将12个layers×12正面重新塑造成144个注意力矩阵，因为dist的输入是两个矩阵。直观地说，在一个定义的距离函数中应该有三个属性。(i) $dist(Ai, Ai) = 0$;(ii)距离函数应该是对称的，即$dist(Ai, Aj) = dist(Aj, Ai)$;(iii)如果$Ai$比$Ak$更接近$Aj$，则$dist(Ai, Aj) < dist(Ai, Ak)$。所以对于接下来的距离，我们根据这些要求对其进行修改，并将其归一化为范围[0,1]，便于比较。

4.1 Two Levels of Distances

Token-Based Distance

对于一个输入句子，我们可以提取144个注意力权重矩阵。每个矩阵∈[0,1]n×n，其中n为句子中的符号。然后对于句子中的每个标记，我们得到144个注意向量(∈[0,1]n)。我们可以计算它们的成对距离，并对n个标记平均，以获得一对注意矩阵的最终标量值。

由以下四种基于令牌的距离函数生成:余弦相似度(cos)、皮尔逊相关系数(corr)、JensenShannon距离(JS)和Bhattacharyya系数(BC)。请注意，为了可读性，请参阅附录A，以了解详细的描述、实现和我们的修改。

Sentence-Based Distance

与基于标记的距离不同，这里我们直接测量整个输入句子对应的两个n × n注意力矩阵之间的距离。我们修改了三个度量:距离相关(dCor) (Székely et al.， 2007)、Procrustes系数(PC) (Gower, 1971)和典型相关系数(CC) (Hotelling, 1992)。详情请参阅附录A。

一般来说，基于句子的度量关注给定两个注意矩阵的协方差和/或线性/非线性依赖，而基于标记的度量只关注两个单一的注意向量。

4.2 冗余矩阵的可视化 Visualizing of Redundancy Matrices

我们以带预训练BERT-base的CoLA为例，可视化了基于两组距离函数的冗余矩阵。我们还在附录b中对其他GLUE任务进行了可视化。如图2所示，每个热图使用一个距离函数来显示标准化距离(在1000个选定的CoLA开发数据上的平均值)。每一项都反映了一对注意力头之间的距离。我们可以清楚地看到，基于令牌距离的冗余矩阵中存在着常见的冗余模式。基于句子的距离也有类似的观察结果。

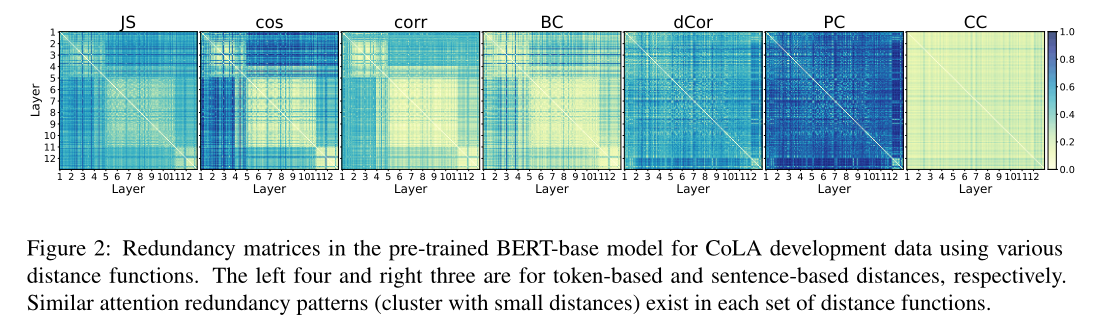
5 Where: 每一层里的冗余 Where: Redundancy in Layers

冗余矩阵中也存在类似的冗余模式。

5.1 Redundancy Patterns

图2中有两个观察结果。首先，注意头在同一层和连续的层往往比分开的头更多余。其次，各层之间存在冗余层次聚类结构。然而，比较两组距离测度的结果，也存在不同的聚类结构。

左边的四个子数字表示基于令牌的距离。他们把前4层、中间6层和最后2层聚成3个簇，最后8层聚成一个更大的簇。最后三个子图是基于句子的度量。集群结构并不比基于令牌的度量更清晰。但我们仍然可以观察到中间10层的距离更小。在同一层的头有更近的距离，特别是第一层和最后一层。

从注意力冗余的角度来看，这些观察结果可以用Kovaleva等人(2019)的结论来解释;Clark等人(2019)认为，在同一层或附近的注意层的头提取类似的特征(例如，任务特定特征)。

5.2 Similar Patterns

接下来，我们将展示当使用四种基于令牌的距离时，会出现类似的冗余模式。以句子为基础的三个距离也是如此。在图3中，我们计算了图2中每一对冗余矩阵(使用CoLA和预先训练的BERT-base)之间的相关性4。在每种类型的距离的冗余矩阵中观察到高相关性。

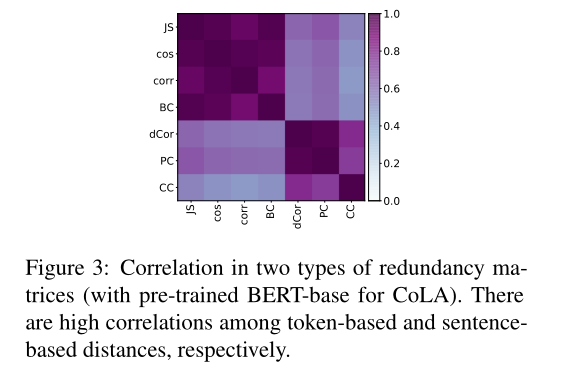
两种类型的冗余矩阵的相关性(与预先训练的BERT-base的CoLA)。基于标记的距离和基于句子的距离分别具有很高的相关性。

6 When: 冗余是阶段独立的 When: Redundancy Is Phase-Independent

图4显示了使用两个距离水平的CoLA的微调BERT-base的注意冗余矩阵(其他任务的结果见附录B)。可以观察到与图2非常相似的冗余模式。

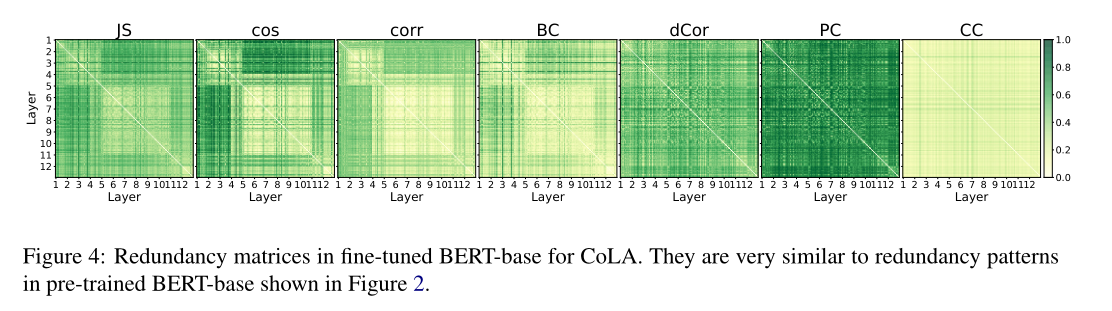
为了量化相似度，我们只需计算图2和图4中两个对应的冗余矩阵的差值的绝对值。平均差值仅为0.035。此外，我们在每个距离函数下计算每个GLUE任务的预训练和微调BERT-base之间的相关性。如图5所示，在所有GLUE任务和所有距离函数的预训练和微调阶段都显示出了高相关性。

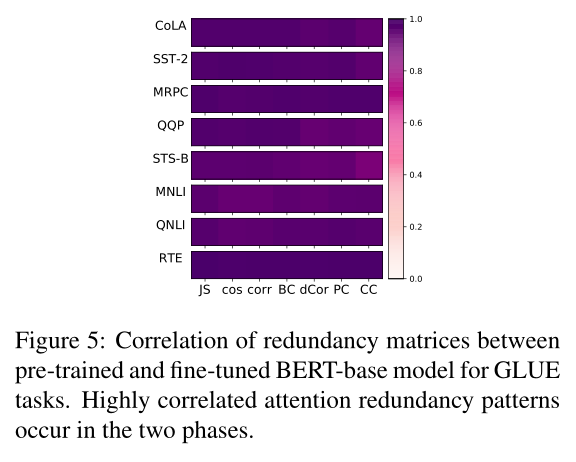
综上所述，预训练阶段和微调阶段的注意冗余模式非常相似，且高度相关。

7 Who: 冗余是任务无关的 Who: Redundancy Is Task-Agnostic

[剪枝策略]

在本节中，我们从面向任务的角度分析了注意力冗余。具体来说，对于每个距离函数和每个阶段，我们计算每对任务的冗余矩阵之间的相关性。经过训练的BERT-base模型在不同距离下的相关性结果如图6所示(微调BERT-base的结果见附录D)。我们发现任务之间的冗余模式非常相似。基于任务类别中提供王et al .(2018),我们也可以注意到相对较高相关性发生在两个栏目中任务(可乐和SST-2),三个相似性和解释任务(MRPC、QQP和STS-B),和三个推理任务(MNLI、QNLI RTE),分别。

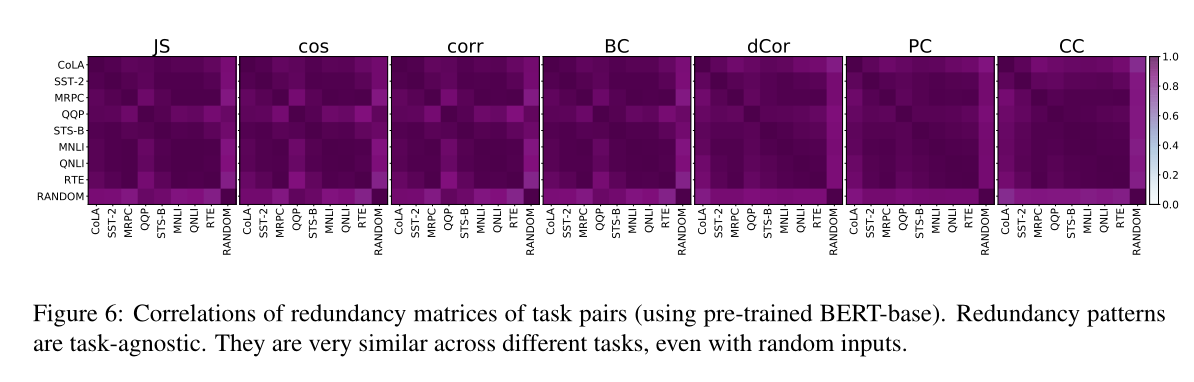
基于这个惊人的发现，我们可以应用这个任务不可知的观察结果来修剪冗余的注意头。在不知道下游任务的任何数据的情况下，接下来我们采用一种简单但有效的基于注意力冗余的聚类zero-shot剪枝策略。

7.1 Case Study Application: Zero-Shot Attention Head Pruning

在本节中，我们介绍了一个简单的zero-shot剪枝策略，基于任务无关的聚类结构的注意冗余矩阵。注意文献中存在一些复杂的剪枝策略。大多数算法都是在微调过程中或微调后将预训练的模型压缩到再调整计算推理阶段的计算负荷。然而，我们提出的剪枝策略是在微调和zero-shot之前(即在不知道微调任务中有任何数据的情况下)。

对现有修剪工程的比较和评价超出了本文的范围。我们把修剪的话题留作以后的工作。然而，我们认为本文中的注意冗余分析有助于开发高效的剪枝方法。

7.1.1 Pruning Method

整个过程如下。首先，我们将随机生成的令牌序列作为BERT-base模型的输入数据，得到如图2所示的冗余矩阵。其次，对单个冗余矩阵或平均冗余矩阵进行聚类。如果给定修剪比$p$，且聚类方法需要给定的聚类数量，则我们将聚类数量设置为$[144 ×(1−p)e]$。否则，优选无聚类数的聚类方法。第三，对每个对象(即注意头)使用聚类优度度量，得到修剪过程中保持的聚类代表头。我们可以简单地删除其他头部对应的可训练参数和后续前馈层中的相关参数，然后像往常一样对下游任务进行微调。

7.1.2 Pruning Performance

在本节中，我们使用了著名的光谱聚类和silhouette Score作为聚类优度度量，获得了聚类代表性头。

我们使用相同的修剪策略来修剪注意力头(因为修剪是零镜头和任务无关的)，并在第3节中对每个带有建议超参数的GLUE任务进行了修剪BERT-base模型的微调。开发集上的微调性能如图7所示。每个子图对应一个任务。x轴为5% ~ 95%的修剪率，间隔为5%。我们为每个微调任务进行10次试验。红色虚线反映了没有修剪的平均性能8。蓝线图显示了不同修剪率下的平均性能。阴影区域的边界覆盖了10个试验中最好和最差的结果。

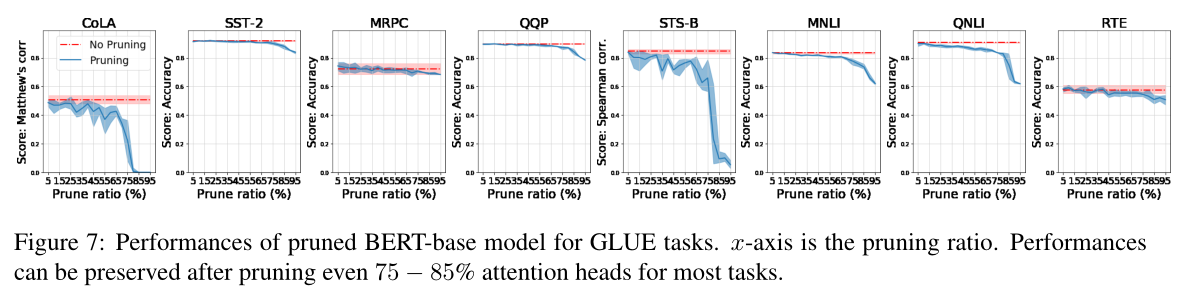
在图7中，性能随着剪枝率的增加而下降，这并不令人惊讶。然而，在这8个任务中，有4个(SST2、MRPC、QQP和RTE)可以使用高达85%的剪枝率，相对于未剪枝模型，没有显著的性能损失(< 5%)。在MNLI和QNLI中，性能损失较大。但是，修剪比率可高达75%，以保证较小的性能损失(< 5%)。仅有的两个异常值是可乐和STS-B。我们认为他们较小的验证集(≤1000)可能会导致波动，使我们无法得出强有力的结论，进一步的研究有待于未来的工作。

7.1.3 Pruning Heads Visualization

在图8中，我们看到了平均超过10次聚类试验的一些修剪结果。较浅的颜色代表一个头修剪得更频繁。当修剪比例较小(例如，<15%)时，前四层的头部被修剪的几率比后面几层的更高。当修剪率增加(25% ~ 75%)时，在较早和较深的层次上的头被修剪得更频繁。然而，有些头像总是保持不变，例如，第11层的头像2、6、10、12，第12层的头像1、3、12。在极端情况下(85%和95%的修剪率)，修剪这些头会损害微调性能(图7)。有趣的是，在所有的修剪率(包括85%和95%的情况)中，中间层中的一些头会保持很高的概率。

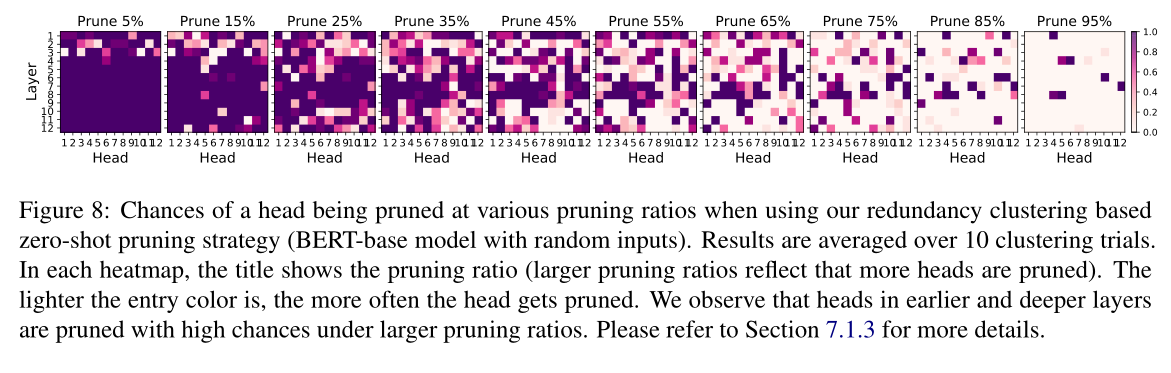
我们观察到头四层的头总是很可能被剪掉。这验证了冗余矩阵中的集群结构(例如，图2)。这可能是因为较早层次的头捕获了更肤浅的语言特征(Kovaleva等人，2019)，这可能比其他头的微调信息更少。随着剪枝率的增加，深层的头部也比中间层的头部更容易被剪枝。我们推测，在中间层之后，上下文化的嵌入对于下游任务已经非常“强大”了。因此，更深层的层不需要太多的头(尽管还剩下一些)来处理任务。

通过对剪枝算法的实例分析，强调了所提出的基于冗余聚类的剪枝方法是一种简单而鲁棒的方法和zero-shot。

(i)与其他修剪方法相比，该方法不需要下游任务的数据;

(ii)从预训练的模型中获得一种剪枝策略，可以鲁棒地剪枝较少的信息头，并对所有GLUE下游任务保持相同的微调性能。

BERT-base模型中存在的阶段无关和任务无关的注意冗余模式使得简单剪枝策略具有强大的优势。作为未来的工作，我们将检验其他多层多头自注意模型是否存在类似的注意冗余模式，并开发相应的剪枝机制。

简短总结 # 你看完这篇论文的总结

作者在这篇文章中用5个W和How提出BERT注意力冗余的问题，并进行了探索。具体包括：

1. What 什么是注意力冗余?
2. How 如何衡量注意力冗余?
3. Where 注意力冗余存在于哪里?
4. When 什么时候出现注意力冗余?
5. Who 谁(哪个任务)有注意力冗余?
6. Why “为什么”阶段独立和任务不可知的注意力冗余会发生?

在4.2章节探索了BERT在预训练阶段的注意力冗余后（使用不同的距离函数进行计算比较），又继续探索了在微调后的注意力冗余情况，发现冗余的模式基本相同（与任务和微调的数据不太相关）。

并从这个结论出发，提出了一个zero-shot的剪枝策略（不需要下游数据），记录了性能。

创新点 # 这篇论文自己写的贡献

1 导言-贡献

优劣 # 论文自己写的和你认为的优劣势（相比其他方法）

1. 从发现比较注意力冗余出发开始，经过分析得到了可以使用zero-shot剪枝策略方法的想法，并且测试得到了比较有效的效果，过程比较完整。
2. 涉及的内容比较多，所以对注意力冗余的机制、原因的探讨比较少，这篇文章中主要写了”Why”章节里讲到的预训练dropout ratio可能带来的影响，更多内容还没有讨论。

流程与公式 # 尽量以图为主，附带必要说明

[7 剪枝策略]

主要实验 # 重点是比较的表格

7.1.2 Pruning Performance