Pruning 泛读论文笔记
Pruning 泛读论文笔记
目录
| 序号 | Tree | Type | Short | 发表日期 | 会议期刊 | 论文名 | 代码链接 | 备注 |
|---|---|---|---|---|---|---|---|---|
| 1 | Pruning | NLP压缩 | 2019.10.14 | Arxiv | Structured Pruning of a BERT-based Question Answering Model | |||
| 2 | Pruning | NLP压缩 | RPP | 2019.9.27 | Arxiv | Reweighted Proximal Pruning for Large-Scale Language Representation | 稀疏 | |
| 3 | Pruning | NLP压缩 | Mask-BERT | 2020.10.11 | EMNLP 2020 | Masking as an Efficient Alternative to Finetuning for Pretrained Language Models | CODE_LINK | |
| 4 | Pruning | 模型分析 | Analysis | 2020.2.19 | ACL 2020 | Compressing BERT: Studying the Effects of Weight Pruning on Transfer Learning | CODE_LINK | Workshop |
| 5 | Pruning | 模型分析 | 2020.5.1 | EMNLP 2020 | When BERT Plays the Lottery, All Tickets Are Winning | |||
| 6 | Pruning | NLP压缩 | MvP | 2020.5.15 | NIPS 2020 | Movement Pruning: Adaptive Sparsity by Fine-Tuning | CODE_LINK | |
| 7 | Pruning | NLP压缩 | IMP | 2020.7.23 | NIPS 2020 | The Lottery Ticket Hypothesis for Pre-trained BERT Networks | ||
| 8 | Pruning | NLP压缩 | 2021.12.10 | NIPS 2021 | Pruning Pretrained Encoders with a Multitask Objective | |||
| 9 | Pruning | 互信息,压缩 | 2021.8.28 | EMNLP 2021 | Layer-wise Model Pruning based on Mutual Information | 使用互信息,选择最小的特征维度,然后基于此进行权重裁剪 | ||
| 10 | Pruning | NLP压缩 | BlockPruning | EMNLP 2021 | Block Pruning For Faster Transformers | CODE_LINK |
1 - Structured Pruning of a BERT-based Question Answering Model
论文内容
摘要
这篇文章研究了在基于BERT和RoBERTa的QA系统里,通过对底层Transformer进行参数结构化剪枝(structured pruning)。发现了一种成本较低的对特定任务进行结构化剪枝和知识蒸馏的混合方法,并且也不需要预训练蒸馏,就能在速度和精度均有的情况下有很好的性能表现。从SQuAD 2.0和Natural Questions的完整模型上开始,引入了能单独消除Transformer中特定部分的门(gates)。
具体研究了:(1)通过结构化剪枝减少每一层Transformer里的参数。(2)在基于BERT和基于RoBERTa的模型上的适用性。(3)对SQuAD 2.0和Natural Questions的适用性。(4)将结构化剪枝的方法和蒸馏的方法结合起来。
得到的结果是在Natural Questions上提高了一倍的速度,只损失了不到0.5的F1分数。
5 结论
作者研究了基于Transformer的各类MRC模型的剪枝方法,发现注意力头的层(attention head layers)和前向传播层(feed forward layers)能在很小的精度损失下被很好地剪枝。
发现相比”Gain”方法,”L_0正则化”的剪枝方法对Transformer的这两个部分更有用。
不需要重新预训练,只需要使用特定任务的训练数据就能剪枝,这个花费和微调差不多,比预训练的花费小很多。
1 引言
提到了NLP的QA任务中,一个新的领域,机器阅读理解(Machine Reading Comprehension, MRC),它的目标是阅读和理解给定的文本,然后在此基础上回答问题。MRC很难加速,但是蒸馏在MRC上的应用效果不太好,表1中比较了两种著名的BERT压缩方法,Distil-bert 和 TinyBert的F1分数。
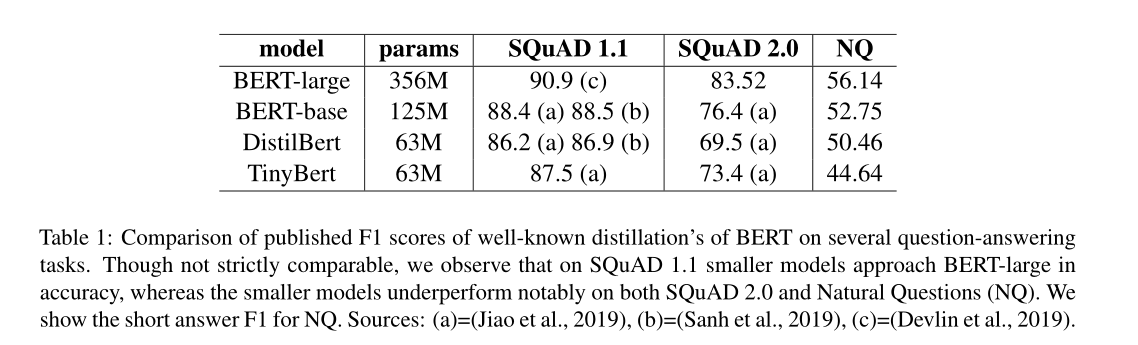
本文的主要贡献是:
- 将结构化剪枝技术应用于前馈层的隐藏维度,而不仅仅是注意头
- 蒸馏和剪枝的结合
- 以最小的准确性损失和相当大的速度显著剪枝MRC系统,不需要重新预训练
2 相关工作
主要关注MRC的蒸馏、剪枝模型-Distil-bert, TinyBERT, MobileBERT。
对BERT的剪枝忽略了MRC任务。
另一些方法忽略了在较低层中文本和查询之间的注意力机制。
3 Pruning transformers
3.1 Gate placement
作者的剪枝方法就是在Transformer中插入额外的可训练的参数,遮罩(masks),每个mask的取值$\gamma _i \in (0, 1)$,决定是否使对应的切片生效。插入了两种类型的mask。
- 在每个自注意层里放置一个mask,决定每个注意力头是否起作用。
- 在每个前向传播层里放置一个mask,决定ReLU/GeLU的结果是否起作用。
3.2 Determining Gate Values
作者研究了四种确定mask gate的值的方法:
- 随机:每个$\gamma _i$的取值都从参数为$\alpha$的伯努利分布取出来,$\alpha$是手动调节的,控制稀疏性。
- Gain方法:通过每个$\gamma _i$作为一个连续的参数并计算均值来估计每个$\gamma _i$对整个训练集的似然$L$的影响。
在每次传递的时候对$g_i$设置阈值,确定保留哪些Transformer。
- L0正则化:$\gamma _i$采样自:

hard-concrete distribution $hc(α_i)$ (Maddi-son et al., 2017) ,$\alpha _i$是通过优化目标函数$L$来训练的:
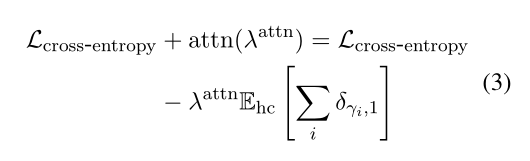
预训练门参数的成本和微调差不多。
3.3 Structured Pruning
$\gamma _i$通过上述的方法之一确定后,对模型进行剪枝。去掉$\gamma _i ^{attn} = 0$的注意头,和前向传播层中$\gamma _i ^{ff} = 0$的切片。
3.4 Extended training

4 Experiments
在SQuAD 2.0和NQ数据集上评估了作者提出的方法。
SQuAD 2.0是一个维基百科文章问题的数据集,是由人类注释者在查看这些维基百科文章时提出的。 NQ是一个谷歌搜索查询的数据集,这些查询的答案来自人类注释者提供的维基百科页面。
实验想研究几个问题:
- BERT-base的剪枝中学到的技术(超参数等)在BERT-large上适用吗?
- 这些技术在不同数据集上是通用的吗?
- 合并蒸馏目标是否能改进作者模型的能力?
4.2 SQuAD 2.0
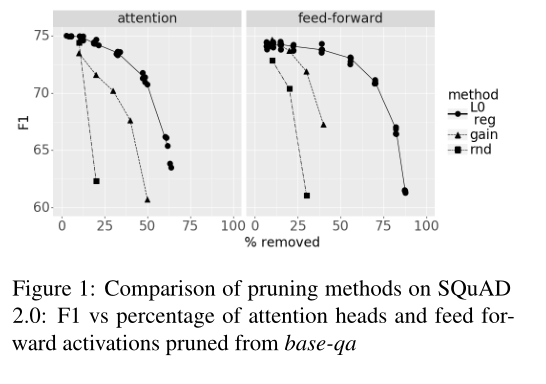
作者在自己训练的BERT-qa模型上用不同的方法得到mask的取值,并比较他们的性能:
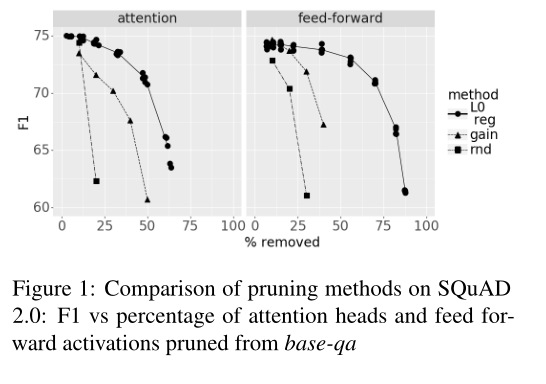
“random”的表现突然衰减。“gain”更好。”L0正则化”的效果是最好的,在48%的剪枝率下只减少了5 F1-points。
在图2中,我们显示了剪枝后剩余的注意力头和前馈激活的百分比。我们看到中间层保留得更多,而接近嵌入和接近答案的层被修剪得更多:

表2中的参数在上面给出。
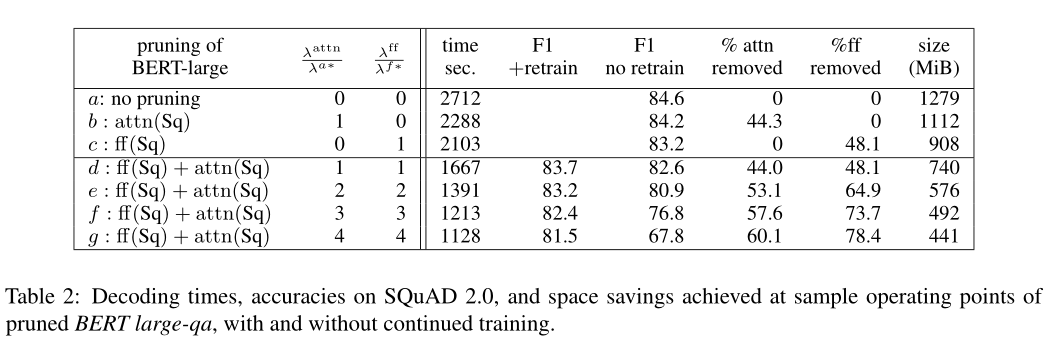
4.3 Natural Questions
研究三个问题:
- 为SQuAD 2.0任务开发的剪枝技术是否适用于NQ任务:4.3.1
- BERT的剪枝是否也适用于RoBERTa?4.3.2
- 能否结合蒸馏和剪枝,得到更小、更快的模型?4.3.3
A1:继续使用上述在SQuAD 2.0上剪枝后的BERT-large模型,并使用相同的模型继续在NQ数据集上继续训练。这个模型记为$retrain(NQ)$。表3表示尽管没得到最好的结果,但也很优秀了。可以认为在剪枝任务里去掉的BERT冗余的参数不是针对特定任务的,而是具有鲁棒性的。
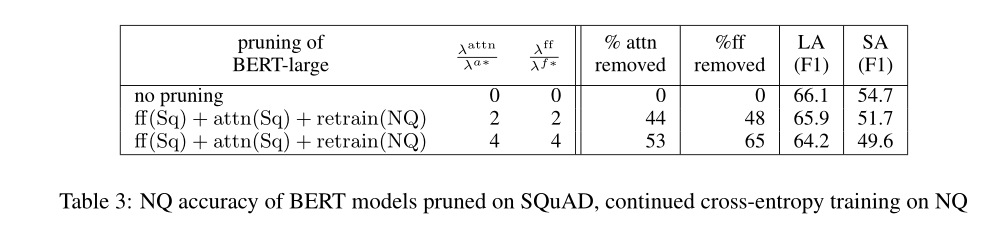
A2:RoBERTa在各种任务的精度上得到了比BERT更好的结果。RoBERTa和BERT有相同的拓扑结构,只是在标记、训练的过程中略有不同,所以对BERT的剪枝方法对RoBERTa也应该起作用。对RoBERTa-large NQ模型进行剪枝,用了相同的方法,使用L0正则化决定masks/gates的取值,表4展示了结果,表明RoBERTa也可以用这样的技术进行成功的剪枝:
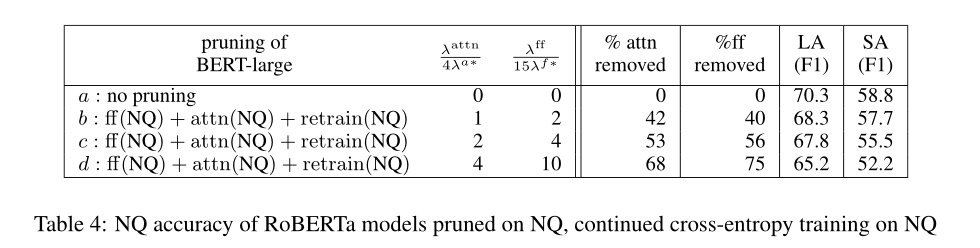
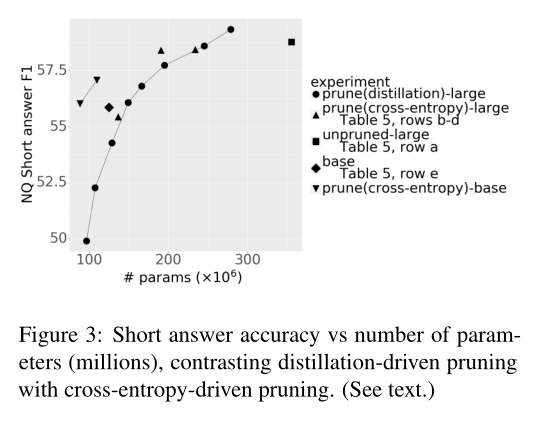
A3: 将精馏和剪枝相结合的最简单方法是,在模型被剪枝后,将继续训练(retrain(nq))替换为具有蒸馏目标的继续训练(蒸馏(nq))。这里,未修剪的模型充当教师,修剪过的模型充当学生。在表5中,我们显示了仅在继续训练阶段使用蒸馏的结果。
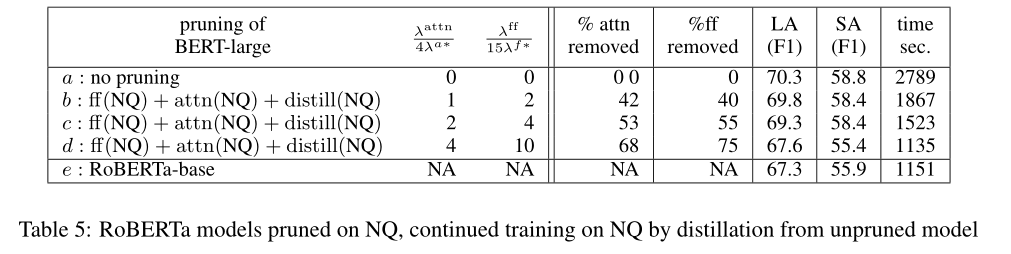
图3里的base点是RoBERTa-base(表5的e)位于剪枝+蒸馏的左上方,表明剪枝+蒸馏的过程并没有完全实现充分潜力。
简短总结 # 你看完这篇论文的总结
本文尝试了在Transformer的前向传播层和注意力头层这两个位置上的结构化剪枝策略。
剪枝的主要方法是:给attn层和ff层都引入一个参数mask,$\gamma _i$,经过L0正则化后去掉该参数为0的对应的层。比较了’随机’、‘gain’、‘L0正则化’后实验结果表明L0正则化得到mask参数的效果最好。
在后续进行了从SQuAD 2.0到NQ数据集的迁移,和BERT到RoBERTa模型的迁移,探究这种剪枝策略是否有普适性。后续进行了蒸馏和剪枝的结合实验,探索效果如何。
文章的具体做的事情感觉可以用实验章节提出要探究的三个问题来表示:Pruning 泛读论文笔记
得到的结果是在Natural Questions上提高了一倍的速度,只损失了不到0.5的F1分数。
创新点 # 这篇论文自己写的贡献
优劣 # 论文自己写的和你认为的优劣势(相比其他方法)
- 本文做的实验都是基于机器阅读理解(Machine Reading Comprehension, MRC)这一个任务(感觉不是很全面?),和Distil-BERT和TinyBERT进行了比较。
- 本文做了从SQuAD到NQ数据集上的迁移,以探索这样的剪枝策略是否具有普适性。具体的做法是在SQuAD剪枝后的模型(提供mask的参数)直接继续进行NQ的学习和剪枝。觉得想法是合理的,不知道做法是否合理。
- 感觉4.3.3的蒸馏+剪枝结合的实验结果图表示,这样的操作至少在MRC任务上是不如RoBERTa-base的,作者说这表明这种方法没有完全实现充分潜力?这是说它这么做不太好吗?因为感觉没提到这样做的好处是什么(推理速度?继续压缩?)这合适吗?
流程与公式 # 尽量以图为主,附带必要说明
主要实验 # 重点是比较的表格
2 - Reweighted Proximal Pruning for Large-Scale Language Representation
论文内容
摘要
这篇文章提出了一种新的剪枝方法Reweighted Proximal Pruning (RPP),该剪枝方法是专为大规模语言表示模型设计的。
在SQuAD和GLUE数据集上的实验表明,高剪枝率下的BERT仍然在预训练任务和下游微调任务中有着很好的准确率。
RPP提供了一个新的视角来帮助分析大规模语言表示可能学到的东西。此外,RPP使得在一系列不同的设备(手机、边缘设备)上部署大型的语言表示模型(如BERT)成为可能。
5 结论
本文提出了一种RPP剪枝算法,该算法在大型预训练语言表示模型BERT上获得了第一个有效的权值剪枝结果。
RPP在不影响训练前和微调任务性能的情况下,获得了59.3%的权重稀疏。
作者重点研究了预训练DNN模型的剪枝率与下游多任务迁移学习目标的性能之间的关系。我们发现,除了SQuAD之外,许多下游任务允许至少80%的修剪率,而任务SQuAD下的修剪率为59.3%。我们提出的RPP方法为分析大型语言表示模型提供了一个新的视角。
1 引言
大的预训练语言表示模型效果很好,但是太大了,很难部署到计算受限的设备中。本文主要探索两个问题:
Q1: 是否有可能通过权重剪枝来压缩大规模的语言表示,如BERT?
Q2: 权重修剪、预训练模型如何影响下游多任务迁移学习目标的表现?
之前的方法有非结构剪枝(non-structured weight pruning)、结构化(structured)剪枝、过滤(filter)剪枝和通道(channel)剪枝。和CNN类型的模型剪枝不同的是,BERT这样的模型不仅要考虑预训练模型的剪枝效果,还要关注下游微调任务的迁移学习能力。
本文研究了一些不规则的权重剪枝在BERT上的表现,如迭代剪枝(iterative pruning)和一次剪枝(one-shot pruning)。但是发现这些方法无法在收敛的同时保持精度不显著下降。作者认为这种剪枝方法的失败是因为基于l1正则化和l2正则化学习到的稀疏模式不正确。
作者在这项工作中提出了Reweighted Proximal Pruning(RPP),由两部分组成:Reweighted l1最小化和近端算子(proximal operator)。重加权l1最小化是比l1正则化更好的稀疏性生成方法。通过近端算子可以使求解稀疏模式(sparsity pattern)和求解训练梯度的过程解耦。
这样第一次得到了在BERT上有效的权值剪枝方法。实验结果表明,在包括SQuAD和GLUE在内的各种下游任务中,都保持了较高的精度。
贡献
作者总结的贡献有以下几点:
- 开发了一种剪枝算法RPP,在大型预训练模型BERT上获得了第一个有效的权值剪枝结果。在不影响预训练和下游任务的情况下,获得了59.3%的权重稀疏。
- 重点研究了预训练DNN模型在下游迁移任务下的性能区别。发现除了SQuAD之外,许多下游任务允许至少80%的剪枝率,SQuAD只有59.3%。
- 观察到随着预训练模型的剪枝率增加,下游任务的性能下降。在不同的任务中下降的范围不同,但是比起基于迭代剪枝的方法,RPP方法都能达到高的剪枝率。
- 和图像分类任务重的剪枝不同,RPP有助于发现BERT中结构化稀疏模式。此外还研究了网络剪枝对BERT中嵌入语言表示的影响。
2 相关工作
介绍了BERT和对多头注意力机制中的一些头进行mask的工作,和作者的工作正交,可以结合起来进一步压缩/加速。
介绍了Reweighted l1和近端算法(proximal algorithm),本文应该是第一次把重加权l1最小化应用到网络压缩,特别是BERT剪枝的工作。
3 RPP during 预训练 for 大体量语言模型
$f_i$表示下游任务中$T(i)\sim p(T)$的损失函数,$p(T)$表示任务的分布。设$w$表示预训练模型的参数,$z_i$表示第$i$个任务指定模型的参数。每个下游任务有单独的微调模型,从预训练模型开始微调,可表示为:
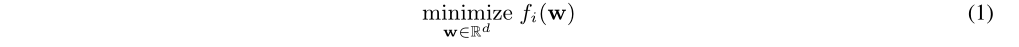
3.1 迁移学习里的剪枝公式化表示
首先考虑常规的权值剪枝公式,在训练前的权值剪枝问题:
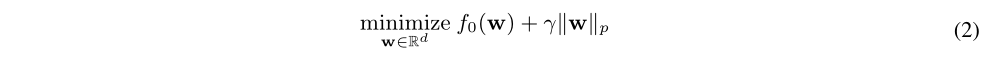
$f_0$表示剪枝的损失函数,$p \in (0, 1)$表示选用哪种正则化,$\gamma $表示正则项
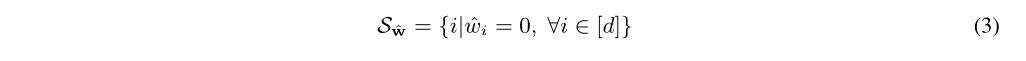
$S_{\hat{w}}$是对公式2求解出来的稀疏模式。
对每个子任务$i$,允许一个额外的微调步骤去训练权值,从$\hat{w}$开始,遵循确定的稀疏模式$S_{\hat{w}}$,即修正后的公式1:
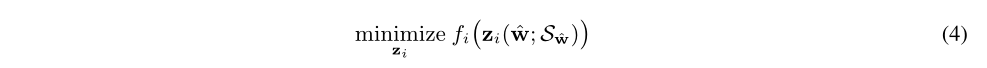
目标是在预训练模型中找出一个稀疏模型,权值集合为$\hat{w}$,在每个子任务上的表现和原来的预训练模型一样好。共享同一个稀疏性$S_{\hat{w}}$。
3.2 RPP
两部分:1. 重加权l1最小化,更好的求解稀疏模式的方法。2. 近似算子,把计算梯度和求稀疏模式分开,不需要每次都在整个sparsity-penalized loss上求解梯度。
3.2.1 重加权l1最小化
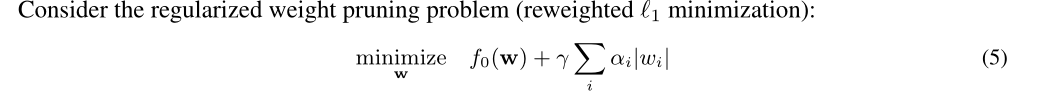
$\alpha _i$表示平衡惩罚的因子。如果$T=1$就退化成了l1稀疏训练。

相比直接l1正则化,这里的公式5会被多次用于求解,迭代去计算更好的$w$和$\alpha$取值,“Reweighted”。
3.2.2 近端算子
近端算法显示,在一组广泛的非凸优化问题上是非常有效的(与原始解相比)。此外,我们提出的重加权’ 1最小化(5)通过近端算子具有解析解。

带近端算子的AdamW优化器算法见附录C的算法3。
为什么选择AdamW而不是Adam?传统的权值衰减在Adam中本质上是无效的,并且对基于梯度的更新有负面影响,这也是自适应梯度算法难以在NLU应用的超深度DNN训练的原因。AdamW是基于Adam通过将权值衰减正则化和基于梯度的更新解耦得到的,避免了过拟合,广泛应用于大型预训练语言模型。RPP的设计思想也受到这个的启发。
4 实验
作者做的不包括RPP部分的工作baseline:NIP(New Iterative Pruning)能够剪枝BERT,在附录A中。用作对比。

RPP算法的具体流程,附录B。

比较了NIP和RPP两种baseline下的MLM和NSP任务(预训练)的准确性和剪枝率。
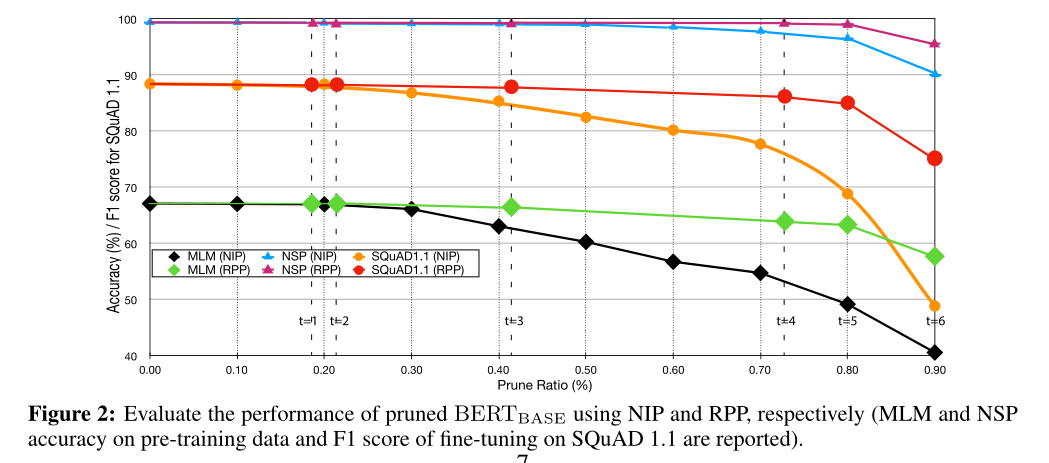
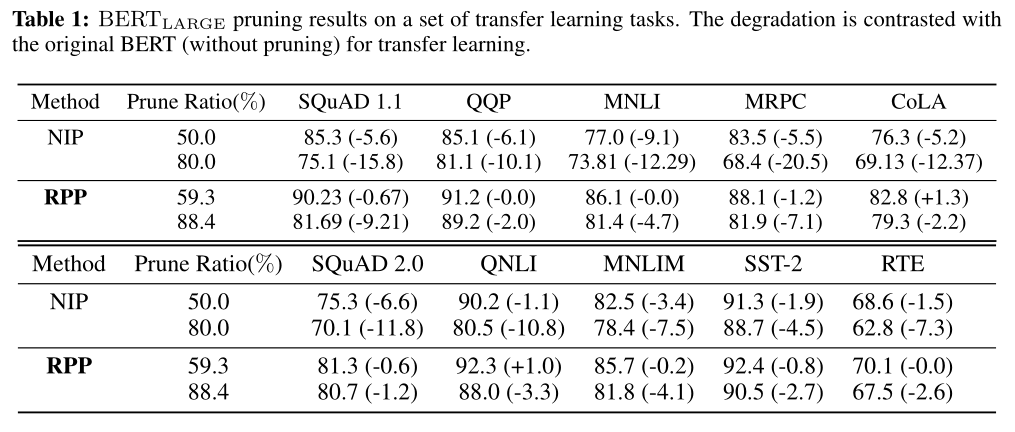
在BERT-large上比较了NIP和RPP两个baseline在不同迁移任务上的表现:
4.3 对BERT的注意力模式可视化
剪枝后的BERT-base模型中取样6个矩阵,进行比较:
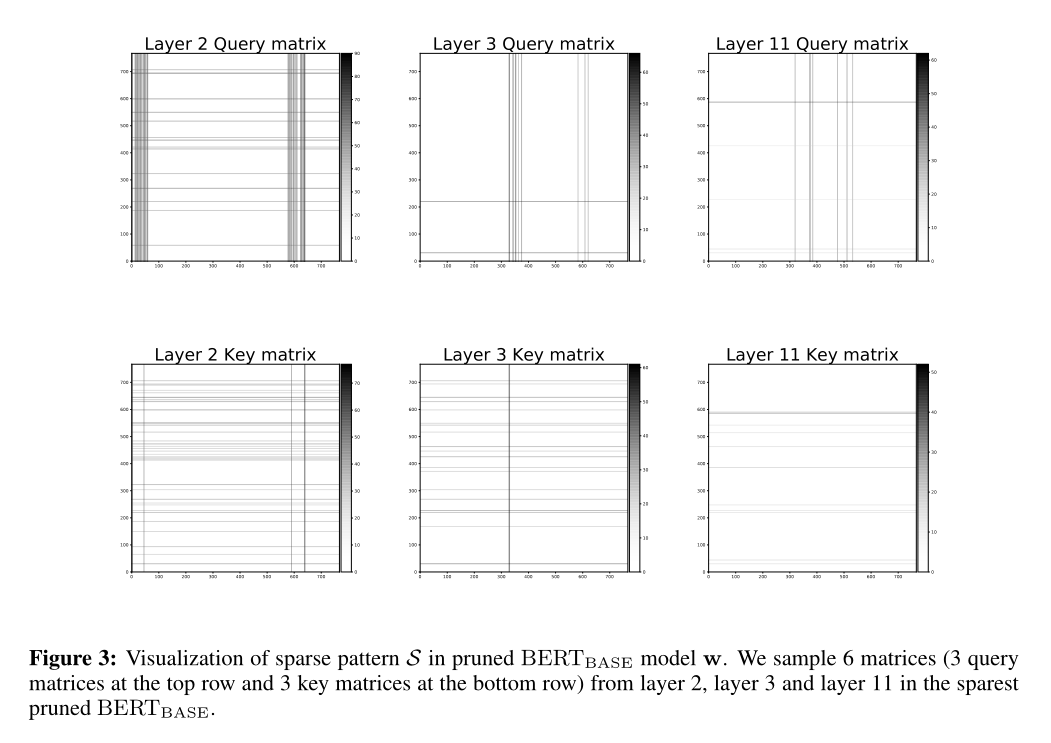
Structured Pattern:作者表示剪枝后的Transformer产生了有趣的群结构(group-wise structures)。和图像分类器上的不规则剪枝不同,这体现了语言模型剪枝的特殊性。作者认为重加权l1方法对找到这些细粒度的稀疏模式很重要。
Semantic interpretation(语义解释):剪枝后的Transformer学到了什么,查询矩阵Q对每个序列内部的注意信息进行建模,Key矩阵K主要对上下文的信息进行建模。
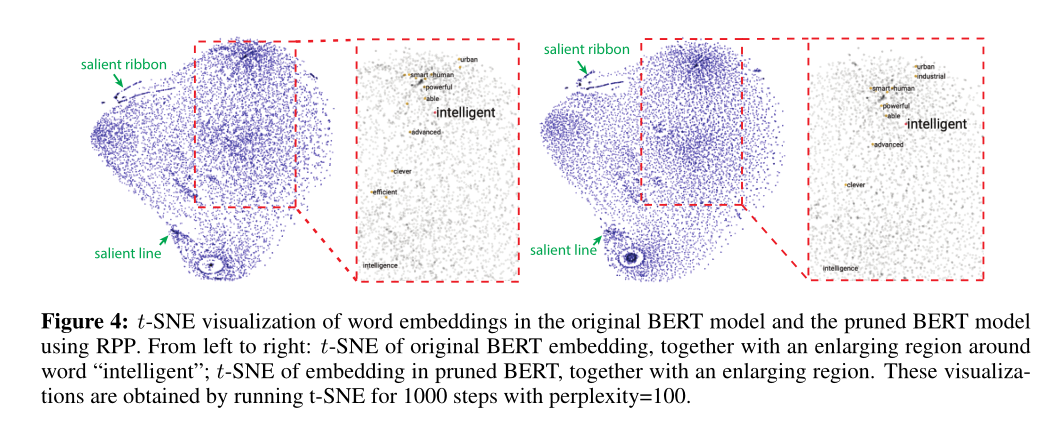
4.4 t-SNE可视化
使用t-SNE可视化比较了剪枝前后的BERT对语言表示的区别。 使用具体的单词”intelligent”为例,RPP的应用保留了与原始BERT相似的大部分语言表示信息。
简短总结
这是首篇对BERT进行了有效的权值修建的剪枝方法,RPP。
RPP由两个重要部分组成:
- 重加权l1最小化,替换了l0、l1正则化,使得在BERT这样的大模型上能进行有效地剪枝(精度不会显著下降),是求解稀疏性更好的办法。
- 近端算子。通过近端算子可以使求解稀疏模式(sparsity pattern)和求解训练梯度的过程解耦。
作者比较了RPP和没使用RPP的工作baseline,NIP。得出RPP在相同剪枝率下在预训练和各种下游任务上都有更好的表现,表示这是一个更有效的剪枝方法。
并且通过剪枝后的矩阵取样和t-SNE可视化分析了BERT这种语言表示模型可能学到的东西。
创新点
优劣
- 是第一个能有效剪枝BERT这样的预训练大语言表征模型的方法。
- 在得到剪枝结果后,对BERT这样的语言模型可能学到的东西给出了一定的讨论。
流程与公式
主要实验
3 - Masking as an Efficient Alternative to Finetuning for Pretrained Language Models
论文内容
摘要
我们提出了一种利用预训练语言模型的有效方法,通过为预训练的模型权重学习可选的二进制掩码(selective binary masks),而不是通过微调权重修改它们。
在11个不同的NLP任务上对掩蔽BERT、RoBERTa和DistilBERT进行了评估,结果表明,掩蔽方案可以获得与微调相当的性能,然而在多个任务需要推断时,内存占用要小得多。
内在评估(Intrinsic evaluations)表明,二进制掩码语言模型计算的语言表示模型编码包含了解决下游任务所必需的信息。
分析loss的情况,发现通过掩蔽和微调的模型都能达到几乎一样的精度。这证实了掩蔽也可以作为替代微调的一种有效方案。
7 结论
作者提出掩蔽masking这样的方法去替代微调去做下游任务。在BERT/RoBERTa/DistilBERT这样的预训练模型上都可用。每个任务不会修改参数,而是只训练一些二进制掩码来选择关键参数进行保留。大量实验表明在NLP各种任务上掩蔽和微调的性能相当。但是在需要解决多个任务的时候,掩蔽可以在不改变预训练参数的情况下提高内存效率。
代码在https://github.com/ptlmasking/maskbert
1 引言
微调简单,性能好,但是需要调优的参数太多,比如BERT-large中就有3.4亿个参数。这是这些模型广泛部署的主要障碍。微调的模型会占用更大内存,需要解决多个任务的时候,需要保存几个大体积的微调模型进行推断。
最近的工作指出了固定模型中搜索神经结构的潜力,代替微调调优的步骤。受这些启发,提出了掩蔽,在预训练上的模型进行训练,选择对下游任务重要的权值,丢弃不相关的权值。
取得了相当的性能。在参数上更高效,只需要保存一组1位的二进制掩码,而不需要保存所有的32位浮点参数,这样能在边缘设备上解决多个任务。
贡献
- 引入了掩蔽这种利用预训练语言模型的新方案,可以替代微调。性能相当。
- 对掩蔽进行了实证分析,揭示了在11个不同NLP任务中取得良好表现的关键因素。
- 研究了loss的情况,揭示了为什么掩蔽具有和微调相当的性能的潜在原因。
3 方法
3.1 Transformer和微调的背景介绍
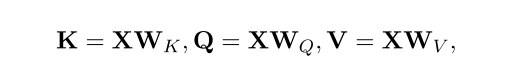
输入的句子是$X\in R^{N\times d}$,$N$是最大的句子长度,$d$是隐含维的大小,$W_K, W_Q, W_V$用来计算X的转换。$X$的自注意力通过以下计算:
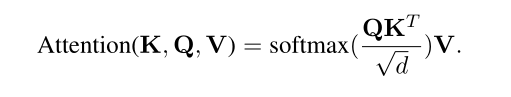
当对下游任务进行微调的时候,将随机初始化一个线性分类器层$W_T$进行投影。放在预先训练的线性层$W_P$(pooler)上更新所有参数,最小化cross-entropy。
3.2 Learning the mask
将每个线性层$W^l \in \lbrace W^l_K, W^l_Q, W^l_V, W^l_{AO}, W^l_O, W^l_I \rbrace$都连接到一个实数矩阵$M^l$,该矩阵从均匀分布中初始化,和每个线性层有同样的大小,然后通过一个基于元素的阈值(二值化器)为$W^l$获得一个二进制掩码$M^l_{bin}$。
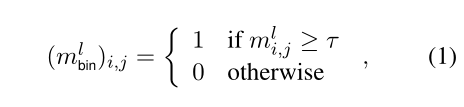
每次前向训练的时候,二值掩码通过Hadamard积(两个相同的矩阵对应位置相乘)求得:
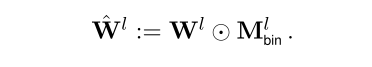
在后向训练中,不能直接通过loss更新二值化,使用噪声估计量来更新$M^l$

通过公式1得到一个屏蔽线性层$\hat{W^l}$,再随机初始化一个相关的$M^l$作为一个额外的线性层,放在预训练模型上面。在训练过程中通过公式2更新每个$M^l$。
在训练结束后把每个$M^L_{bin}$保存下来以供以后推理,与微调后的参数相比,仅需要3%的内存。嵌入层也不必被隐藏, 这会进一步减少内存消耗。
作者主要提到了$M^l_{bin}$初始化的稀疏性和选择哪些层去mask会造成影响,在第5节中展开讲。
5 实验
5.1 初始稀疏度的影响
在四个任务上分别使用(1%,3%,5%,10%,…95%)初始稀疏度进行实验。别的超参数相同。每个实验都用不同的随机种子重复4次。
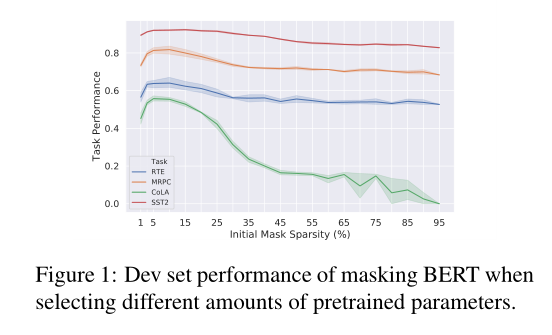
结论:1. 在初始稀疏度较大,去除了大部分预训练参数的情况下会使性能较差,是因为预训练的知识都被丢掉了。2. 逐步降低稀疏度,通常在3%-10%之间会产生合理的结果。在更大的数据集上更不敏感一些。3. 选择几乎所有的参数,会影响性能。初始化保留过多参数会阻碍优化。
5.2 每层做了什么 Layer-wise behaviors
神经网络层里,句法信息在底层表示得更好,语义信息在高层表示得更好。因此简单屏蔽所有的Transformer blocks可能是不理想的。
研究了mask应用于不同层的任务性能。分别探究了从下往上和从上往下的。

观察到:
- 大多数情况下自上而下的掩码优于自下而上的掩码。所以在低层次中选择所有预训练的权值是合理的。
- 于自底向上掩蔽,增加掩蔽层数可以逐渐提高性能。
- 在自顶向下掩蔽中,随着掩蔽层数的增加,CoLA性能提高,而MRPC和RTE不敏感。回想一下,CoLA测试的语言可接受性通常需要句法和语义信息。所有的BERT层都涉及到表示这个信息,因此允许更多的层进行更改应该会提高性能。
5.3 比较掩蔽和微调
性能比较。表1报告了11个NLP任务在开发集中屏蔽和微调的性能。我们观察到,将掩蔽应用于BERT/RoBERTa/DistilBERT可以获得与微调相当的性能。
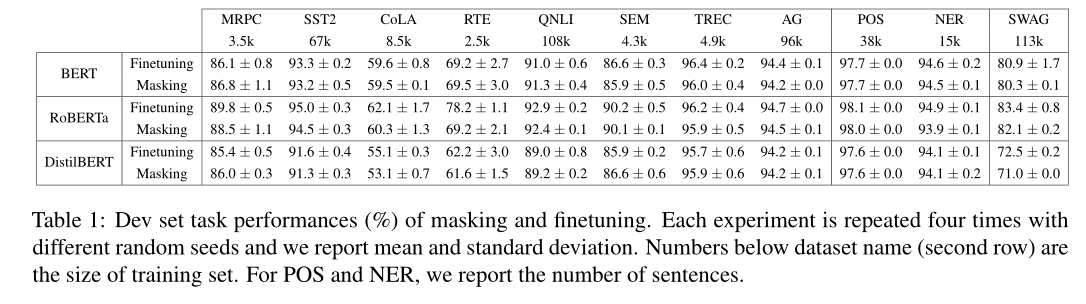
内存比较。已经证明了掩蔽和微调的任务性能是可以比较的,接下来我们将演示掩蔽的一个关键强度:内存效率。

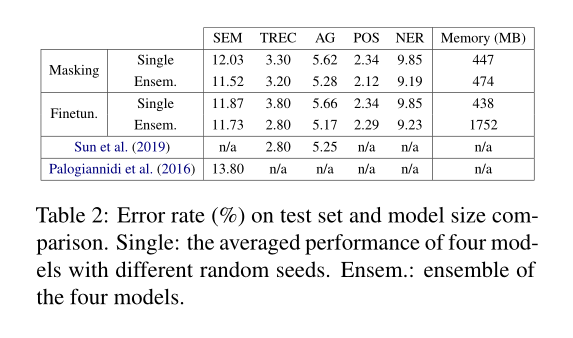
简短总结
用训练掩蔽的参数去替代了微调的过程。这样就可以在相同的预训练模型上引入不同的参数去做不同的任务,对内存的利用效率会高得多。
在需要解决多个任务的时候,掩蔽可以在不改变预训练参数的情况下提高内存效率。
创新点
优劣
- 我觉得mask的训练方式能有效可能是因为BERT的参数太多了,尤其是相比特定任务的输出数量上来说。其中去掉一些可能会造成负面影响的效率确实会有用。觉得这篇文章比较有创意性。
- 给掩蔽相比微调在性能以外找到了另外一个这么做的好处——内存效率。
流程与公式
主要实验
4 - Compressing BERT: Studying the Effects of Weight Pruning on Transfer Learning
论文内容
摘要
探索BERT的权值剪枝,并提出了一个问题:预训练时进行的压缩会如何影响后续的迁移学习?
我们发现,剪枝在三个不同程度上对迁移学习的影响。(1)低程度的剪枝(30-40%)根本不会影响预训练的loss,也根本不会影响到下游任务。(2)中等程度的剪枝会增加预训练的损失,并阻止有用的预训练信息传递到下游任务。(3)高程度的剪枝还会阻止模型拟合下游数据集,导致进一步的退化。
观察到对特定任务进行微调BERT并不能提高其可被剪枝的能力。我们的结论是,BERT可以在预训练的时候进行剪枝,而不需要对每个任务单独进行剪枝,因为这样不会影响性能。
7 结论
于量级权值修剪,我们已经证明了30-40%的权值不编码任何有用的归纳偏差,可以丢弃而不影响BERT的普适性。 其余权重的相关性因任务的不同而不同,对下游任务的微调不会通过改变被修剪的权重来改变这种权衡的性质。
1 引言
预训练的模型通常比单独在下游数据上训练的模型具有更高的准确性。 训练前范式虽然有效,但仍存在一些问题。虽然有人声称语言模型前训练是一项“通用的语言学习任务”,但这并没有理论依据,只有经验证据。
从头开始训练BERT-Base需要花费约7000美元,并排放约1438磅二氧化碳。
本文研究的主要问题:压缩BERT是否会影响其向新任务的迁移能力?微调是否使BERT更容易压缩?
贡献
我们的研究结果如下:
- 低水平的修剪(30-40%)根本不会增加训练前的损失或影响向下游任务的转移。中等水平的剪枝增加了训练前的损失,并阻止有用的训练前信息传递到下游任务。这一信息对每一项任务并不同样有用;任务随着训练前损耗的增加而线性下降,但速率不同。
- 根据下游数据集的大小进行高水平的修剪,可能会阻止模型拟合下游数据集,从而进一步降低性能。
- 最后,我们观察到,对特定任务的BERT进行微调并不会提高其剪枝能力,也不会显著地改变剪枝顺序。
据我们所知,之前的工作还没有表明BERT是否可以以任务通用的方式压缩,既保留了训练前的好处,又避免了多次压缩和重新训练BERT的昂贵实验。
3 实验
基于公共BERT库进行了BERT剪枝实验,代码在https://github.com/mitchellgordon95/bert-prune
我们对一个训练好的BERT-Base模型进行了权值修剪我们以10%的增量从0%到90%选择稀疏性,并在训练的前10k步中逐渐将BERT修剪成这种稀疏性。 图1中表示了不同方式的剪枝在各个剪枝比例下的准确度。
介绍了实验中BERT的参数和数据集等内容。
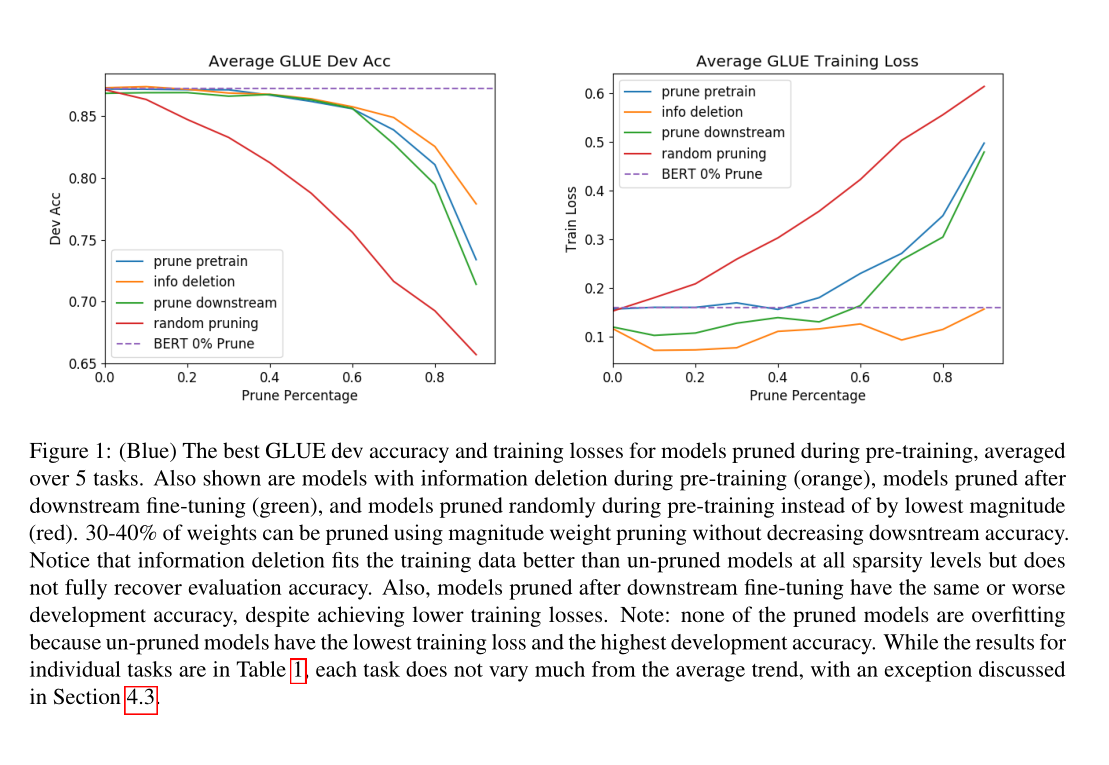
4 剪枝方法
4.1 30-40%的剪枝
图1显示,通过量级权重修剪后的前30-40%权重不影响任何下游任务的训练前损失或推理。这些权重可以在微调之前或之后进行修剪。 从稀疏架构搜索的剪枝角度来看,这是有意义的:当我们初始化BERT-Base时,我们初始化了许多可能的子网。SGD选择最佳的一个进行训练前训练,并将剩余的权重推到0。然后我们可以在不影响网络输出的情况下删除这些权值。
4.2 中等级别的剪枝
超过40%的修剪,性能开始下降。当我们修剪拟合训练前数据所需的权值时,训练前的损失就会增加(表1)。 隐藏层的特征激活开始偏离低修剪水平的模型(图2)在这一点上,下游精度也开始下降。
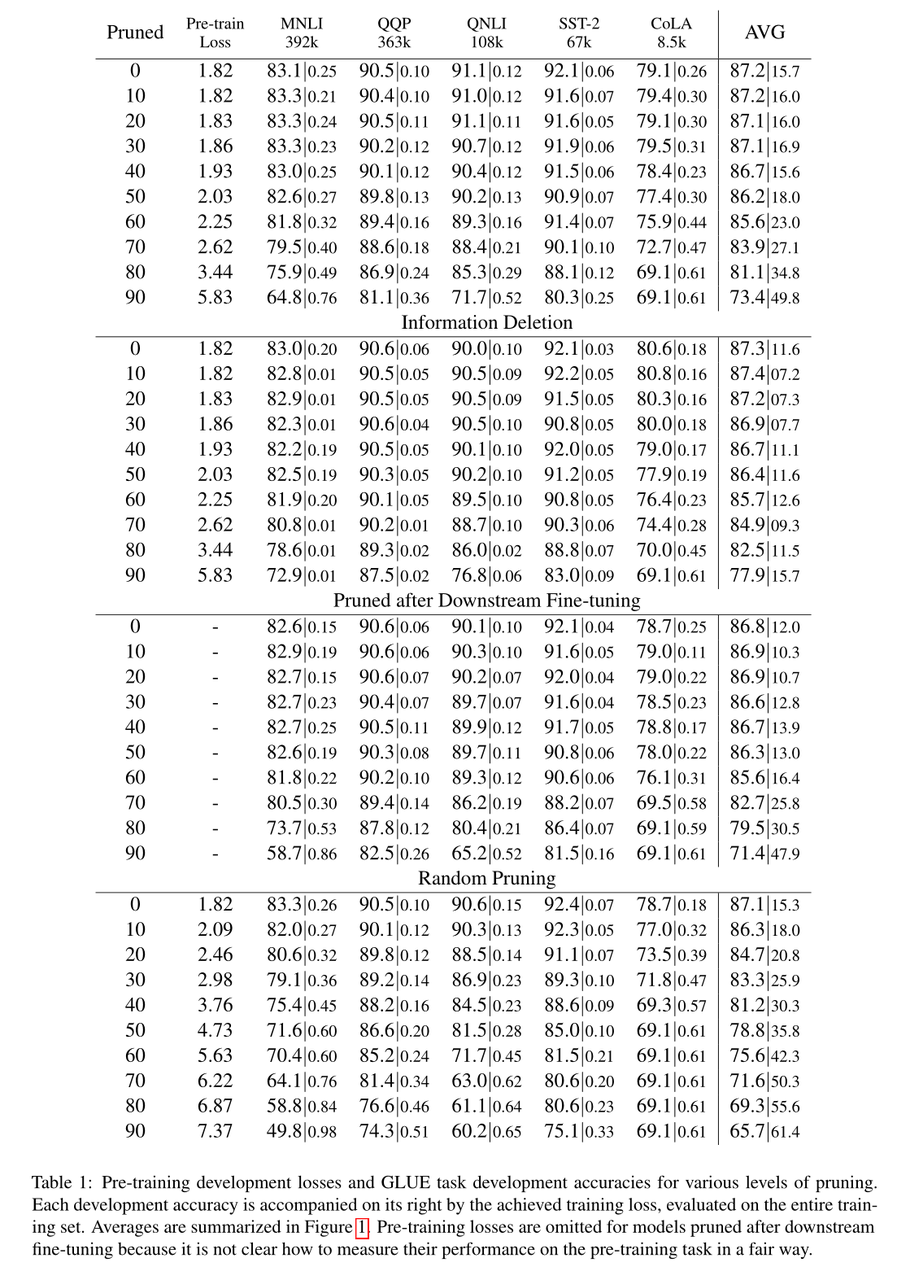
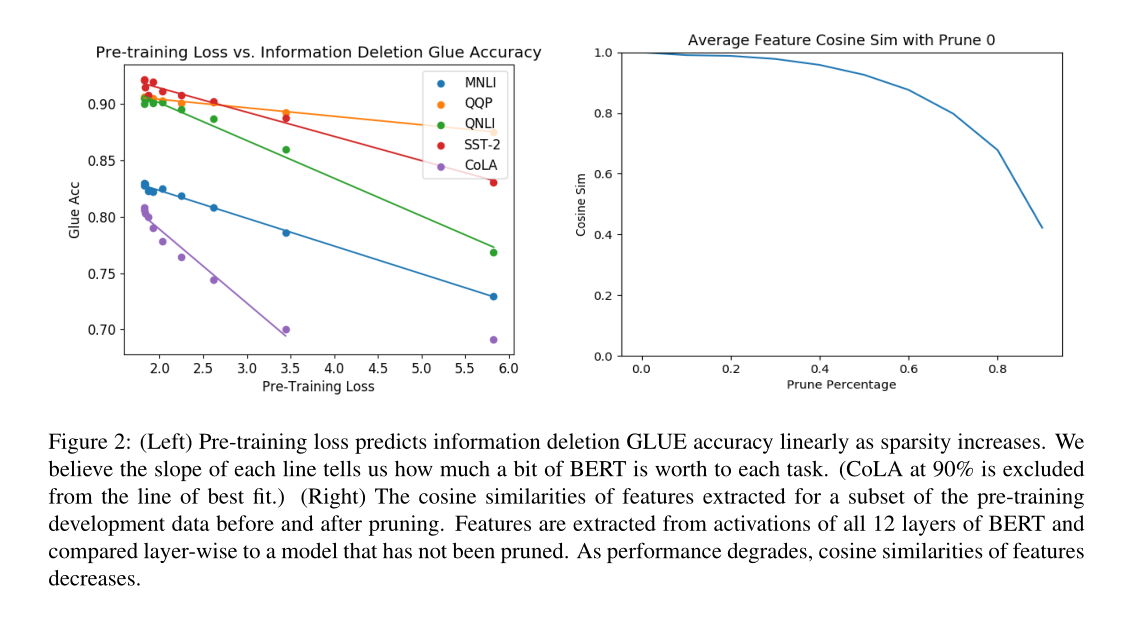
可能影响下游任务的原因:
- pruning通过将权值设为0来删除训练前的信息,防止训练前学习到的有用的归纳偏差的转移。
- 剪枝通过保持某些权值为零来正则化模型,这可能会妨碍下游数据集的拟合。
4.3 高级别的剪枝
当稀疏度达到70%及以上时,带有信息删除的模型恢复了一些精度,所以说明40-60%剪枝后的模型复杂度是导致性能下降的第二个原因。 表1可以看出,对于训练数据量最大的MNLI和QQP任务,信息删除比剪枝效果更好。 相比之下,SST-2和CoLA的模型恢复得不太好,因为它们的数据较少。
4.4 分析被剪枝掉的BERT部分的价值
我们已经看到,过度剪枝的BERT会删除对下游任务有用的信息。图2中表示删掉的部分会线性影响预测的效果。
作者针对不同任务讨论了BERT每个部分的影响。
5 下游微调并不会提高可剪枝性
图4显示,即使经过了下游微调的一段时间后,权值也会迅速地以新的排序顺序重新稳定下来,这意味着较长的下游训练对权值被修剪的影响很小。
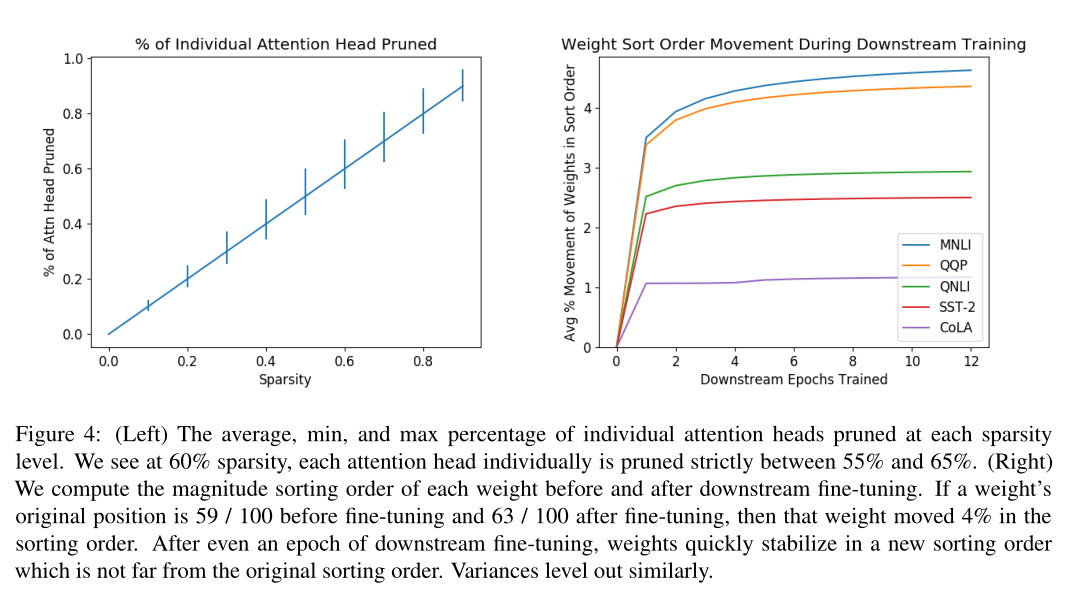
简短总结
本文主要研究的是,在预训练阶段进行剪枝,是否会影响到下游任务的效果?
作者给出的实验结果表示答案是否,也就是说只要在预训练模型剪枝好后再进行特定任务的微调即可,不会导致效果变得更差。
以及给出了不同的剪枝程度下进行实验的结果和讨论,分析造成这种结果的原因可能是什么。
创新点
优劣
- 感觉是实验的总结和分析,给出的结论是预训练剪枝和下游微调的关系影响,主要在描述这种实验中观察到的现象。
- 把剪枝的方法按照剪枝的比例分成了低中高三个阶段,从而得到高程度剪枝的效果比中程度高一点是因为中程度剪枝的复杂性影响了结果,这个结论是不是有点不太有道理。
流程与公式
主要实验
5 - When BERT Plays the Lottery, All Tickets Are Winning
论文内容
摘要
基于Transformer的大型模型被证明可以简化为更小数量的自注意头和层。我们从彩票假设的角度来考虑这一现象,使用了结构化(structured)和量化(magnitude)剪枝。
对于微调后的BERT,我们发现(a)有可能找到性能与完整模型相当的子网络,(b)从模型其余部分取样的类似大小的子网络性能更差。
使用结构化修剪,即使是最坏的子网络也仍然是高度可训练的,这表明大多数预先训练的BERT权值是潜在有用的。我们也研究了好的子网络,看看它们的成功是否可以归因于卓越的语言知识,但发现它们不稳定,不能用有意义的自我注意力机制来解释。
7 结论
本研究使用了基于量化的和基于重要性的剪枝方法对BERT微调中的彩票假设进行验证。 对于这两种方法,我们发现只有经过修剪的“好”子网才能达到与完整模型相当的性能,而“坏”子网则不能。 然而,对于结构化剪枝,即使是“坏”的子网也可以分别微调以达到相当强的性能。这说明好的子网在微调中是不稳定的,所以不能把“好”归功于自注意力机制。
这表明,大多数预先训练的BERT在微调方面可能是有用的,它的成功可能更多地与优化表面有关,而不是特定的语言知识。
1 引言
我们从彩票假设的角度,对GLUE任务上的BERT微调进行了系统的案例研究。我们对BERT自注意头的基于量化的权重剪枝和基于重要性的剪枝进行了实验和比较,我们将其扩展到BERT中的多层感知器(MLPs)。
贡献
发现:
- 使用这两种技术,我们发现“好”的子网达到了全模型性能的90%,并且比从模型其他部分取样的类似规模的子网性能好得多。
- 在许多情况下,即使是“坏”的子网也可以重新初始化为预训练的BERT权值,并分别进行微调以获得较强的性能。
- 在微调的随机初始化中,“好的”网络是不稳定的,而且它们的自我注意头并不一定编码有意义的语言模式。
2 相关工作
彩票假说:Lottery Ticket Hypothesis
“密集的、随机初始化的前馈网络包含子网络(中奖彩票),在单独训练时,这些子网络在类似次数的迭代中达到与原始网络相当的测试精度”。 然而,到目前为止,LTH的工作主要集中在“获胜的”随机初始化。
3 方法论
实验都基于Transformer库中的BERT-base lowercase上完成的。 它对9个GLUE任务进行了微调,并使用表1所示的指标进行了评估。所有的评估都是在开发集上完成的,因为测试集不是公开发布的。每个实验我们随机测试5个种子。
BERT基本上是transformer编码器层堆起来的。每个层都有一个多头注意力机制(a multi-head self-attention,MHAtt),后面跟着一个MLP,每个省周围都有残差连接。
每个MHAtt都由一堆确定的参数决定。 MHAtt是输入x的每个头的输出之和:
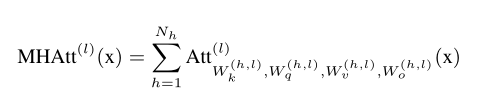
3.1 量化剪枝
对于量级修剪,我们对每个任务的BERT进行微调,并在整个模型中迭代地修剪10%的最小量级权重(不包括嵌入,因为本工作的重点是BERT的权重)。我们在每次迭代中检查开发集的分数,只要性能保持在完整的微调模型性能的90%以上,我们就会继续剪枝。
3.2 结构化剪枝
研究了BERT结构块的结构化剪枝,并在约束条件下对其进行了掩模处理。 我们在一次向后传递中计算head和MLP的重要性分数,删除10%的head和一个得分最小的MLP,直到开发集的性能在90%以内。
4 BERT Plays the Lottery
我们将大小剪枝和结构剪枝分别称为m-剪枝和s-剪枝。 图1显示了QNLI的“好”子网的热图,即在修剪后保留90%的全模型性能的子网。
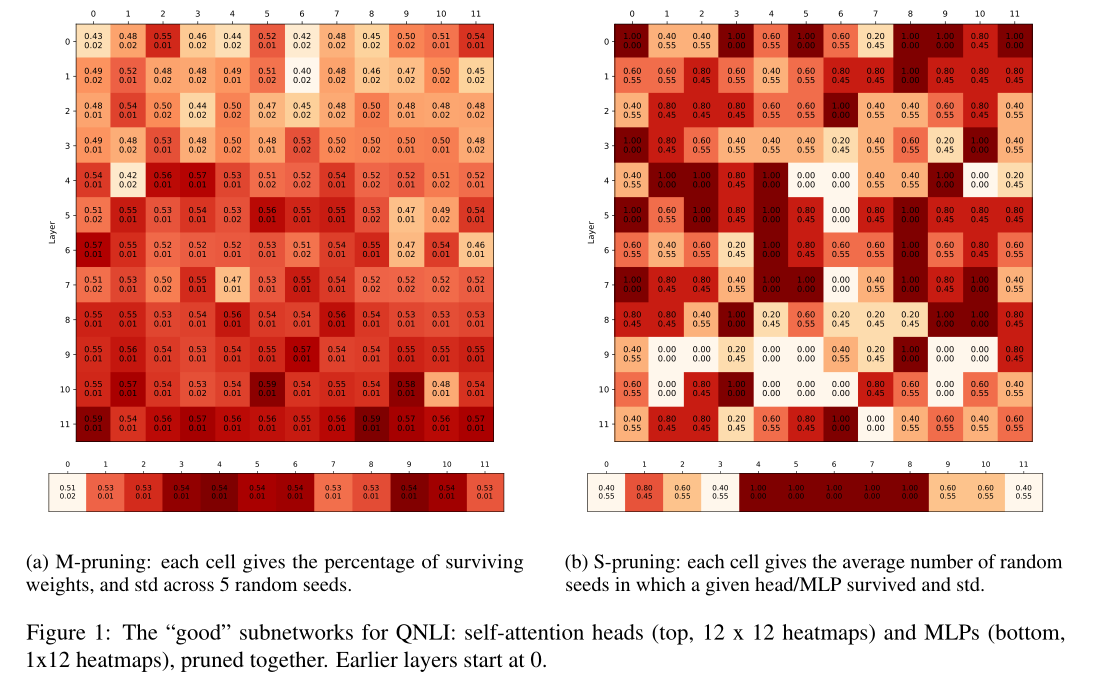
对于s-pruning,我们展示了一个给定的头/MLP在剪枝中幸存下来的随机初始化的数量。对于m-pruning,我们计算了所有GLUE任务(不包括嵌入)中BERT头和mlp中存活权值的百分比。
图1a显示,在m-pruning中,所有的架构块都丢失了大约一半的权值(42-57%的权值),但较早的层被修剪得更多。使用s-pruning(图1b),最重要的头部往往在较早和中间层,而重要的mlp则更多地在中间。请注意,Liu等人(2019)还发现,中间的Transformer层是最可转移的。
图1b,将头部和mlp修剪在一起。当它们被单独修剪时,总体模式是相似的。当它们被单独修剪时,保留的头(或MLPs)更少(头为49%比22%,MLPs为75%比50%),但将它们一起修剪总体上更高效(即产生更小的子网)。 这个实验暗示了BERT的自注意头和mlp之间的相当大的相互作用:随着可用的mlp减少,模型被迫更多地依赖自注意头,从而提高它们的重要性。
4.2 在BERT微调上测试LTH,彩票假说
LTH预测,从零开始训练的“良好”子网应该能够匹配完整的网络性能。我们使用以下设置进行实验:
- “好”子网:通过两种技术从完整模型中选择的元素;
- 随机子网:与“好”子网大小相同,但元素是随机从完整模型中取样的;
- “坏”子网:从那些没有通过修剪的子网中取样的元素,加上一个剩余元素的随机样本,以匹配“好”子网的大小。
选择这些子网络是为了很好地处理这些特定的数据,而相应的“坏”子网络仅与“好”子网络相关。因此,我们不期望这些子网络可以推广到其他数据,并且相信它们可以最好地说明BERT在微调中“学到”的东西。
每个子网络类型的性能如图2所示。主要的LTH预测得到了验证:“好的”子网可以单独成功地进行再训练。观察到的m-pruning和s-pruning的区别如下:
- 对于9个任务中的7个任务,m-pruning比s-pruning能获得更高的压缩(比s-pruning多10-15%的权重)。
- 虽然m-pruned子网更小,但它们大多能达到全网络性能。对于s-剪枝,“良好”的子网大多略低于完整的网络性能。
- 可以预期随机抽样的子网的性能比“坏”的好,但比“好”的差。这是m-pruning的情况,但对于s-pruning,它们的性能大多与“好”子网相当,这表明随机样本中的“好”头/MLPs子集足以达到完全的“好”子网性能。
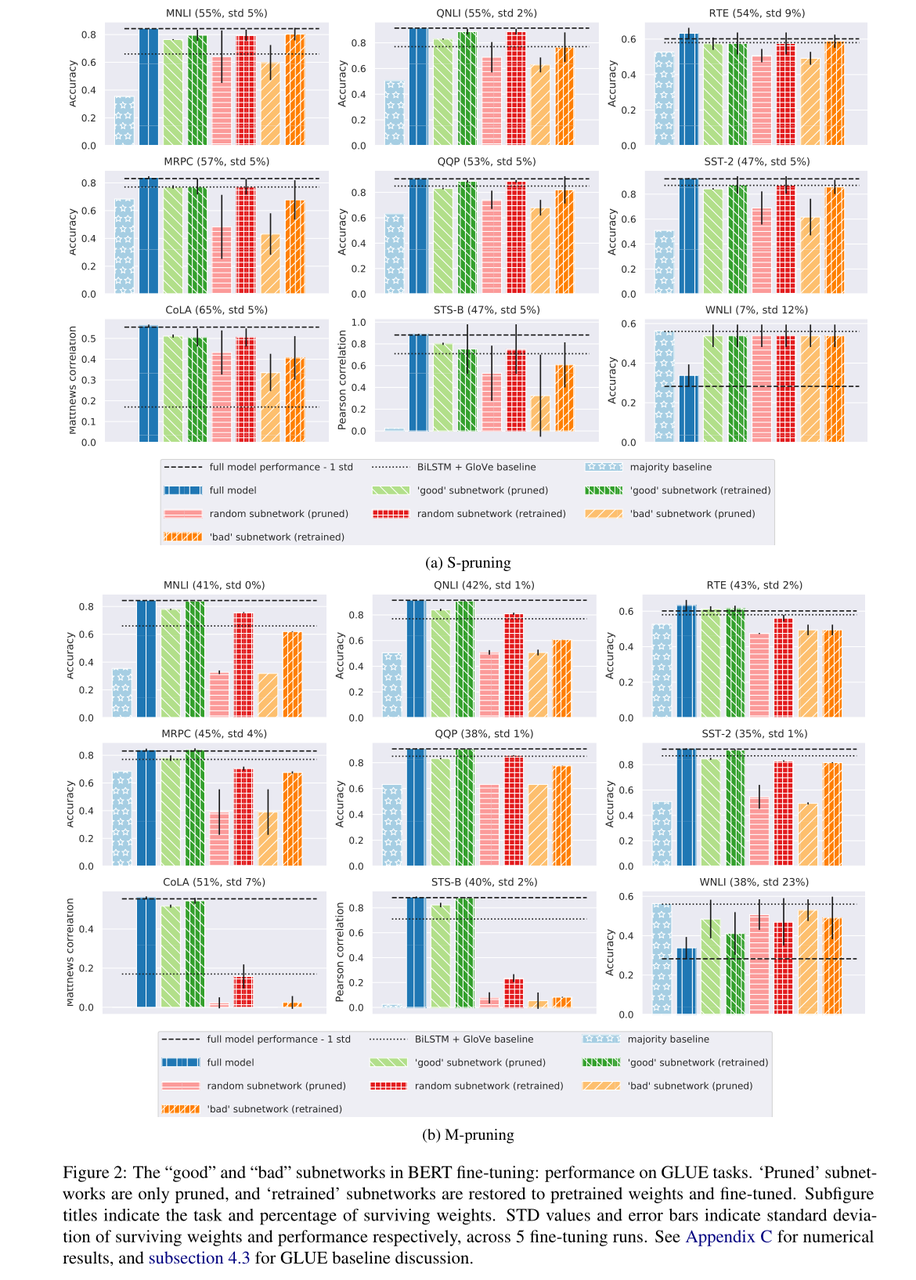
4.3 坏的子网有多坏?
表2显示了使用这两种方法进行修剪和重新微调的“坏”子网的结果,以及Wang等人(2018)对三个GLUE基线的开发集结果。在6/9的任务中,经过m-修剪的“坏”子网络比经过s-修剪的子网络至少落后5个点,在相关任务(CoLA和STS-B)上尤其糟糕。
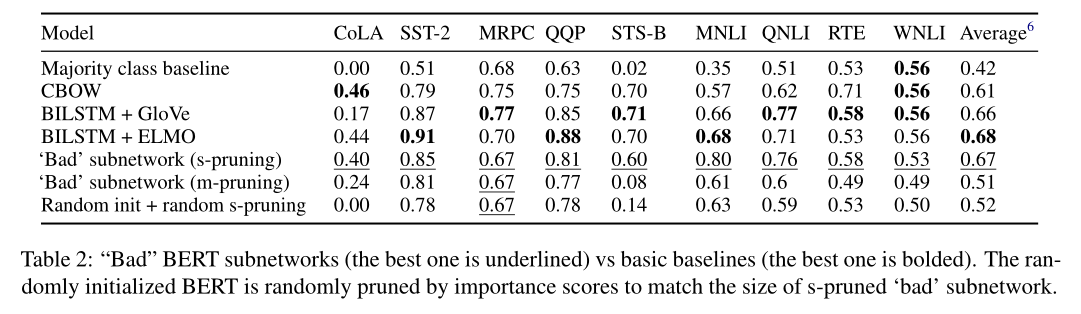
我们随机初始化BERT,并应用随机s剪枝掩码,以使其与s剪枝的“坏”子网保持相同的大小。显然,即使这个模型在原则上是可以训练的(仍然超过大多数类的基线),但平均来说,它比预先训练的权重要高出15个点。这表明即使是最糟糕的6GLUE排行榜也会使用宏观平均指标来对参与系统进行排名。我们只考虑表1中的指标来获得这个平均值。对于给定的任务,预训练的BERT组件仍然包含许多有用的信息。换句话说,一些彩票是“中奖”并产生最大的收益,但所有的子网都有大量的有用信息。
5 对BERT’s 子网的研究
然而,如果更好的性能来自于语言知识,我们将期望“好的”子网更好地编码这一知识,并在相同任务的微调运行中相对稳定。
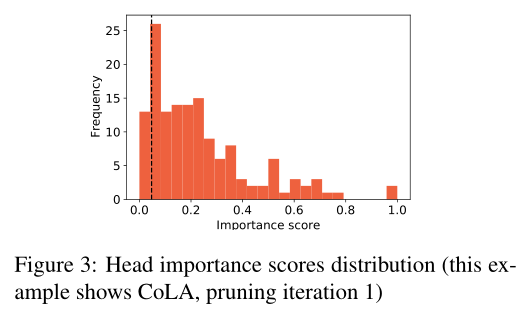
实验结果意味着“好的”子网是不稳定的,并且更多地依赖于随机初始化,而不是对特定任务使用部分预先训练的权值。 图3中显示的重要性分数的分布解释了为什么会出现这种情况。在任何给定的剪枝迭代中,大多数head和mlp都具有较低的重要性值,并且都可以以大致相等的成功率进行剪枝
简短总结
这篇文章使用量化剪枝和结构化剪枝(m-pruning & s-pruning)在BERT上做了不同子网的实验,验证彩票假说LTH。主要的LTH预测得到了验证:“好的”子网可以单独成功地进行再训练。在这个基础上做了很多实验:1. “好的”、“随机”、“坏的”子网单独finetunig的结果比较。2. 比较BERT坏的子网和别的模型的性能。3. 讨论了好的子网可能学到的东西,这部分内容很多。
创新点
优劣
- 在好的子网和坏的子网上可能学到的东西进行了很长篇幅的讨论,进行了很多实验比较。
- 彩票假说这个内容感觉很有意思。
流程与公式
主要实验
6 - Movement Pruning: Adaptive Sparsity by Fine-Tuning
论文内容
摘要
量化剪枝是纯监督学习中一种广泛应用的模型压缩方法;然而,在NLP的迁移学习机制中,它的有效性较低。
我们提出使用运动剪枝(movement pruning),一个简单的一阶(first-order)权值剪枝方法,更适用于预训练的模型进行微调。我们给出了该方法的数学证明,并将其与现有的零阶(zeroth-)和一阶剪枝方法进行了比较。实验表明,当对大型的预训练语言模型剪枝时,运动剪枝可以显著改进高稀疏性。
当与蒸馏相结合时,该方法在只保留了3%模型参数的情况下实现了最小的精度损失。
8 结论
我们考虑了针对特定任务的微调的预训练模型的剪枝情况,比较了零阶和一阶剪枝方法。证明了一种基于直通式梯度的简单的权值剪枝方法对该任务是有效的,并且它适用于使用一阶重要性分值的方法。将这种运动剪枝应用到基于Transformer的结构中,在高稀疏状态下,我们的方法强很多。分析表明了这种方法如何适应微调制度的方式,而量化剪枝不能。
这篇文章是作者在huggingface的工作中的一部分。
1 引言
根据权重的重要性来去除权重的剪枝方法,是一种特别简单有效的模型压缩方法。量化剪枝是其中最广泛应用的方法,它保留了绝对值较高的权重。虽然量化剪枝对于监督学习是非常有效的,但它在迁移学习体制中是不太有用的。
这篇文章提出了运动剪枝,运动剪枝与量级剪枝的不同之处在于,当训练过程中权重值缩小时,无论高值还是低值,都可以进行剪枝。
这种剪枝策略可选0阶和1阶的参数,能让基于微调的目标效果更好。引入了一种简单、确定的运动剪枝方法,进行比较,这种方法基于直行估计器(straight estimator)。
贡献
- 在预训练的BERT上进行剪枝,在一系列不同任务中做实验。发现在高稀疏的区域(小于剩余权值的15%)这种方法相比量化剪枝和其他一阶剪枝(如L0正则化)提升很大。
- 在自然语言推理(MNLI)任务上,剪枝到只剩下5%编码器的权重的模型有原始BERT 95%的性能。
- 通过分析量化剪枝和运动剪枝的差异,发现两种方法的剪枝模型有很大的不同,其中运动剪枝对末端任务的适应能力更强。
3 背景:基于分数的剪枝策略
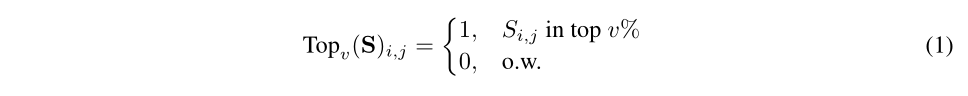
通过保留S矩阵(重要性分值矩阵)前v%的权重进行剪枝。
迭代量化剪枝:先训练模型,直到收敛,然后去掉最小幅度的权值。然后将去除的权值固定为0,对稀疏化的模型进行重新训练。重复此循环,直到达到所需的稀疏级别。

本文中涉及、对比的几种剪枝方法。
4 运动剪枝
量化剪枝可以看作是利用了0阶信息的模型。这项工作中,运动剪枝的重要性是1阶信息。意思是保留的不是远离0的信息(绝对值大),而是保留了训练过程中逐渐远离0(绝对值逐渐变大)的参数。
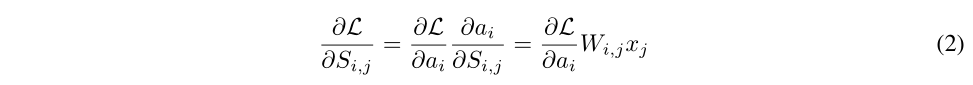
在训练时的loss$L$对$Si,j$的梯度由公式2给出。这意味着更新了权重的分数,即使这些权重在向前传递中被屏蔽。我们在附录A.1中证明了运动剪枝作为一个优化问题是收敛的。
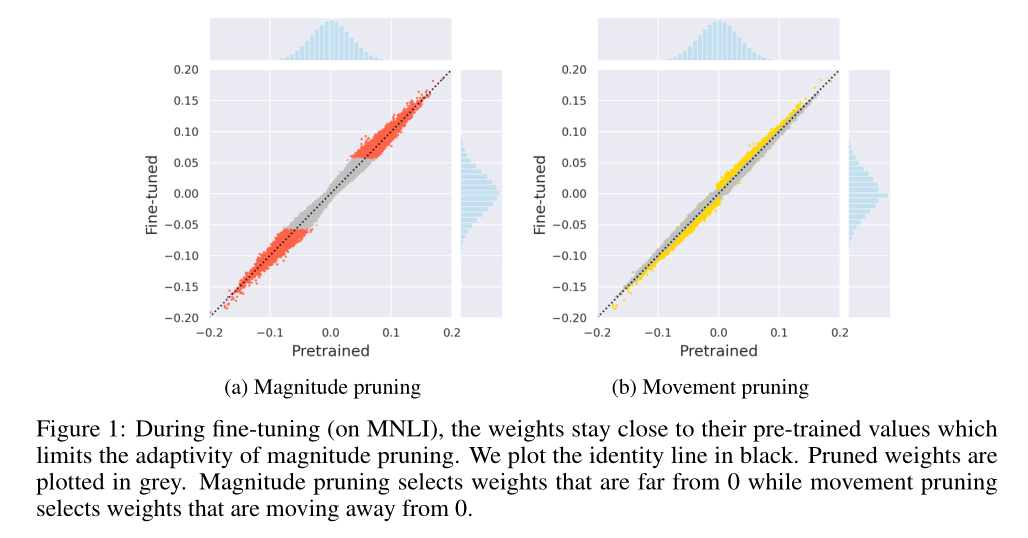
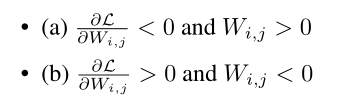
意思就是绝对值变大,重要性$Si,j$也会随着变大。“我们认为,这对该方法的成功至关重要,因为它能够基于特定任务的数据进行修剪,而不仅仅是预先训练的值。”
5 实验
所有报告的稀疏度百分比都是相对于BERT-base的,并且甚至与基线相比,都精确地对应于模型大小。对于给定的任务,我们通过修剪方法对预训练的模型进行微调,以获得相同数量的更新(在6到10个epoch之间)。将三次稀疏调度用于量级剪枝(MaP)、运动剪枝(MvP)和软运动剪枝(SMvP)。在修剪结束时增加几个冷却步骤可以提高性能,特别是在高稀疏状态下。v的进度表为:
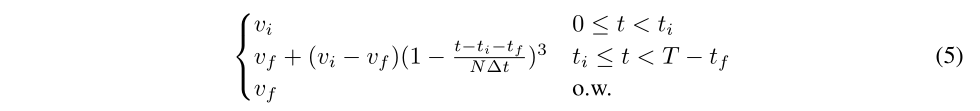
6 实验结果
图2显示了在每个数据集上进行不同级别剪枝的主要剪枝方法的结果。
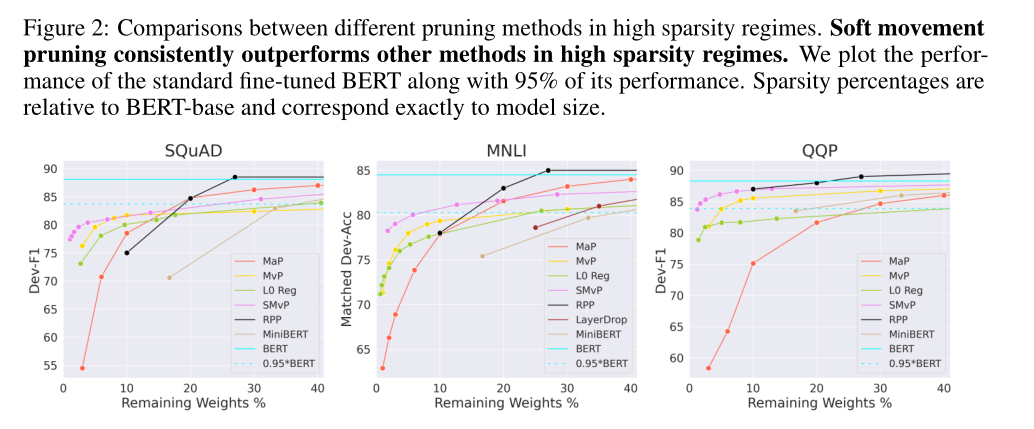
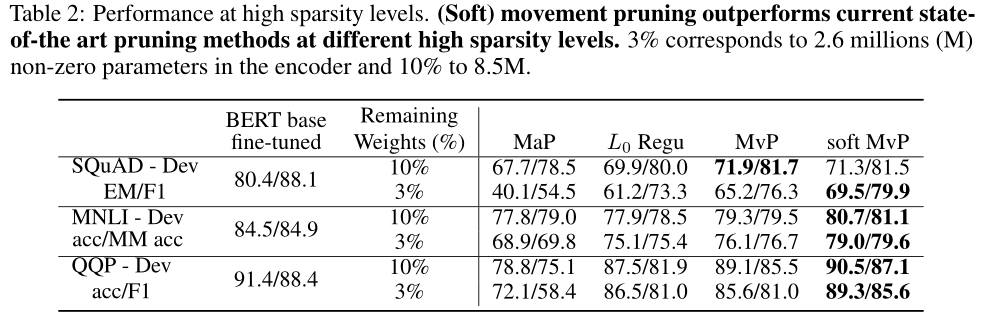
剪枝:在低稀疏度(超过剩余权值的70%)下,相对于密集模型,量级剪枝的性能比所有方法都好,几乎没有损失,而运动剪枝方法的性能即使在低稀疏度水平下也会迅速下降。但在稀疏度较高的情况下,量级剪枝的性能较差,性能下降非常快。相比之下,一阶方法在剩余权值小于15%的情况下表现出很强的性能。
运动剪枝和软运动剪枝与其他基线相比具有良好的性能,但QQP的RPP与软运动剪枝性能相当。运动剪枝也优于微调的迷你bert模型。这与[Li et al., 2020]是一致的:训练一个大模型,然后压缩它,比从头开始训练一个小模型,既高效又有效。
Distillation further boosts performance
在上述工作之后继续使用蒸馏,得到了更好的效果。
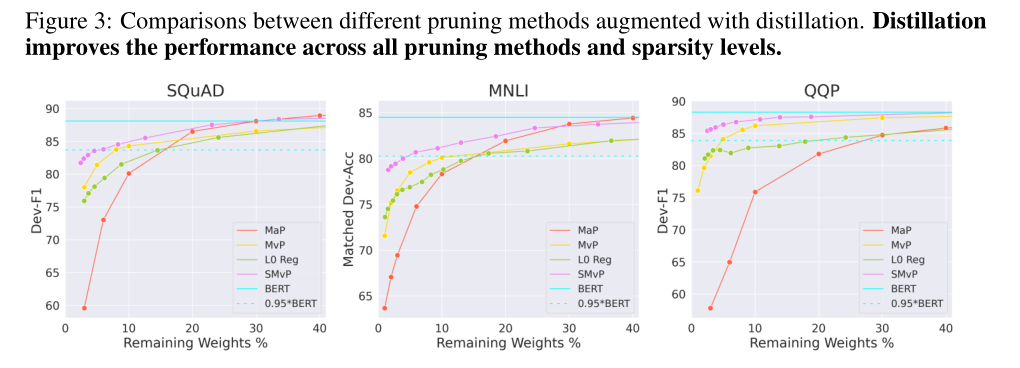
7 分析
运动剪枝适应性更强。
图4a比较了在相同稀疏度下使用幅度和运动剪枝对同一模型的同一矩阵进行剪枝后剩余权值的分布。我们观察到,根据定义,量级剪枝去除所有接近于零的权值,最终得到两个簇。相比之下,运动剪枝可以得到更平滑的分布,它可以覆盖除接近0的值之外的整个区间。
图4b显示了运动修剪中每个个体的权重与其相关的重要性得分。
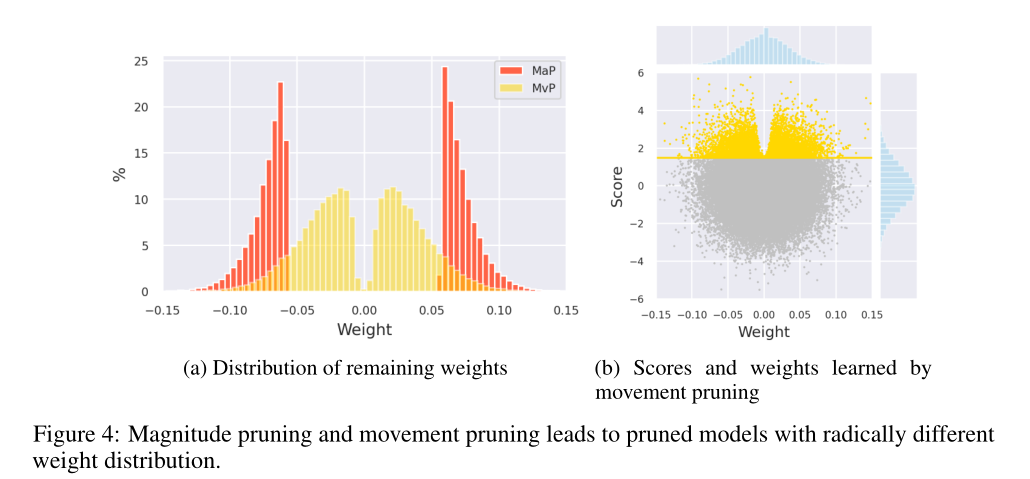
简短总结
本文提出了运动剪枝的方法,作为一种一阶(first-order)剪枝方法,在高稀疏的剪枝下能得到更好的效果,代表性的结果是在MNLI任务上用仅剩5%的权重得到了BERT95%的性能。
主要和量化剪枝进行了对比,前者是在剪枝中保留绝对值较大的,离0较远的权重值,本工作选择的是在剪枝中保留在训练集上逐渐远离0,绝对值变大的权值。作者做了一系列的实验,发现量化剪枝在低程度的剪枝上表现较小,但在高程度的剪枝上明显被运动剪枝打败,作者分析这可能是和运动剪枝能在训练中具有更强的适应性有关,相比量化剪枝,得到重要性分数的策略可能更适用。
创新点
优劣
- 比较了0阶和1阶的剪枝方法,做的实验和比较结果比较全面,在非常高的剪枝率上得到的效果感觉很有说服力,作者提出的运动剪枝更具有适应性的观点似乎站得住脚。
- 在结果后做了很多分析,但是一开始提出的契机是不是有点玄学。。
流程与公式
主要实验
7 - The Lottery Ticket Hypothesis for Pre-trained BERT Networks
论文内容
摘要
对彩票假说(lottery ticket hypothesis)的研究表明,NLP和CV的模型包含更小的子网络,也能够独立地进行准确的训练,并能迁移到其他下游任务上。
在这项工作中,结合这些现象来评估这种可训练的、可转移的子网络是否存在于预训练的BERT模型中。对于一系列下游任务,我们确实发现匹配的子网络具有40%到90%的稀疏性。我们发现这些子网络是在预训练初始化的时出现的。子网络在MLM(与预训练模型相同的任务)上普遍都能迁移;那些在其他任务中被发现的子网络只能在有限程度上迁移。
6 结论
我们在预训练BERT模型的背景下研究彩票假设。我们发现,主要的彩票观察结果仍然成立:使用预先训练的初始化,BERT包含了稀疏的子网,这些子网具有非常的稀疏性,可以在一系列下游任务上进行隔离训练以获得充分的性能。
此外,还有通用的子网络可以传输到所有这些下游任务。这种转移意味着我们可以用一个更小的子网络取代完整的BERT模型,同时保持它的转移到其他任务的能力。
1 引言
在这场规模越来越大的模型竞赛的同时,一个新兴的子领域已经探索了在不牺牲性能的情况下训练更小的子网络来代替完整模型的前景。如果我们知道要选择哪个子网,我们可以从一开始就训练较小的网络。在越来越多关于彩票假说的研究中,出现了两个关键主题:
- 预训练的初始化。 在计算机视觉和自然语言处理的大规模设置中[17-19],彩票方法只能在训练的早期点找到匹配的子网,而不是在随机初始化时。
- 迁移学习。使用彩票方法查找匹配的子网是非常昂贵的。它需要对未修剪的网络进行完整的训练,删除不必要的权值,并将未修剪的权值从训练的早期点倒回它们的值。这比简单地训练整个网络要昂贵得多, 而且,为了获得最好的结果,它必须重复多次。但是,由此产生的子网在相关任务之间传输[22-24]。这个属性使得通过为许多不同的下游任务重用子网来证明这种投资是合理的。
贡献
虽然彩票假设已经在NLP[18,19]和transformer[18,25]的背景下得到了评估,但在BERT预训练的背景下没什么人做,本文主要探究这点。 我们特别关注这些子网络的传输行为,因为我们寻找通用的子网络,可以减少对下游任务进行微调的成本。在本研究过程中,我们有以下发现:
- 使用非结构化的量级剪枝,我们发现在标准GLUE和SQuAD下游任务下的BERT模型中,匹配子网络的稀疏度在40%到90%之间。
- 与以往的NLP工作不同,我们发现这些子网是在(预训练的)初始化时,而不是在经过一定量的训练后。与之前的工作一样,这些子网的性能优于那些随机剪枝和随机重新初始化的子网。
- 在大多数下游任务中,这些子网不会转移到其他任务,这意味着匹配的子网稀疏模式是特定于任务的。
- 使用掩蔽语言建模任务(用于BERT前训练的任务)发现的稀疏度为70%的子网是通用的,并在保持准确性的情况下转移到其他任务。
我们的结论是,从其他计算机视觉和NLP设置的彩票观察扩展到带有预先训练初始化的BERT模型。 在大规模的环境中,只能在训练的早期找到匹配的子网会消失了。 此外,确实有通用的子网络可以替代完整的BERT模型而且可以迁移学习。随着预训练在NLP和深度学习的其他领域变得越来越重要,我们的结果表明,可以从一开始就训练较小网络的令人兴奋的可能性——将成为这类学习算法的范例。
2 相关工作
BERT的压缩。剪枝和知识蒸馏的技术。
NLP中的彩票假说。之前的研究发现,匹配的子网在transformer和lstm训练的早期就存在,但在初始化时并不存在。
3 前言
本节中,我们将详细介绍我们的实验设置和用于识别子网的技术。对子网的介绍:
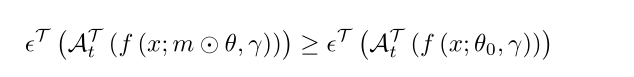
对Winning ticket 和 Universal subnetwork的解释。

迭代训练找subnet的过程。

4 BERT中匹配子网的存在性
我们评估了先前在彩票假设上的工作中提出的四个关于匹配子网的主张:
- 在某些网络中,IMP发现中奖彩票。 有中奖的彩票吗?
- IMP找到的随机剪枝的子网和随机初始化的子网不匹配。IMP中奖的票比随机修剪或初始化的子网稀疏吗?
- 在其他网络中,IMP只找到匹配的子网吗?在训练早期的某个步骤I处,或θi处初始化的子网络优于θ0[17]处初始化的子网络。 重放能提高性能吗?
- 当找到匹配的子网络时,它们与使用标准剪枝找到的子网络在相同的稀疏性下达到相同的精度。 IMP子网的性能与标准剪枝匹配吗?
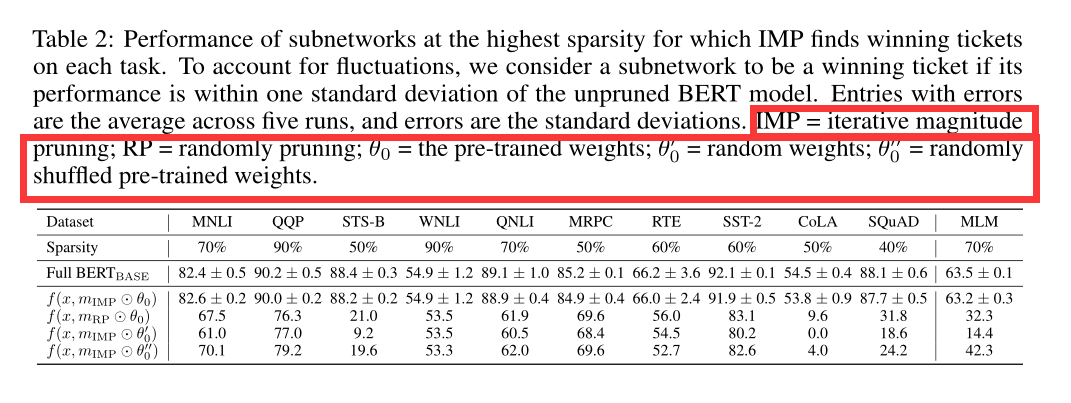
A1: 我们确实为MLM任务和所有下游任务找到了中奖的票(表2)。为了考虑性能的波动,我们认为如果一个子网络的全BERT的性能在一个标准偏差的性能之内,那么这个子网络就是中奖的票我们发现这些中奖彩票的最高稀缺性从40% (SQuAD)、50% (MRPC和CoLA)到90% (QQP和WNLI)不等。每个任务的稀疏性和任务本身的属性(例如,训练集的大小)之间没有明显的关系
A2: 为了在BERT的背景下评估这些主张,我们训练一个子网络f(x;mRP吗?θ0,·)和一个随机修剪掩码(评估修剪掩码mIMP的重要性)和一个子网络f(x;mIMP吗?随机初始化(评估预训练初始化θ0的重要性)。从表2可以看出,两种情况下的表现都远低于中奖彩票的表现;例如,在MNLI上随机剪枝时,它下降了15个百分点,在重新初始化时下降了21个百分点。这确认了该设置中特定修剪权重和初始化的重要性。
A3: 对任何下游任务来说,rewinding不会显著提高性能。事实上,在某些情况下(STS-B和RTE),性能下降如此之多,以至于子网不再匹配,即使我们有两个百分点的差额。这是一个显著的偏离之前的工作,在最坏的情况下重放对精度没有影响。STS-B和RTE的结果特别差的一个可能的解释是,它们的小训练集导致过拟合。
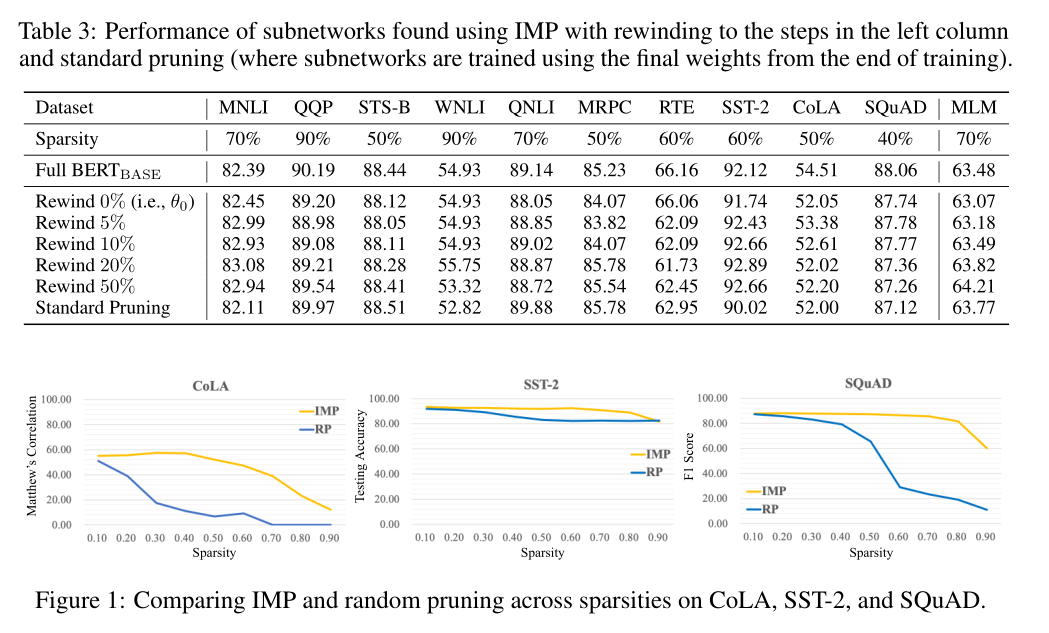
A4: 在表3中,我们看到结果因任务的不同而不同。对于某些任务(QQP, QNLI, MRPC, MLM),标准修剪可以提高中奖彩票的性能高达两个百分点。对于其他(STS-B, WNLI, RTE, SST-2),性能下降高达3个百分点。最大的下降再次发生在具有小训练集的任务中,因为标准修剪可能过拟合。
5 子网的迁移任务
Q1: 中奖的彩票迁移吗?
虽然也有传输性能与相同任务性能匹配的情况,但这是例外。在我们考虑的11个任务中,只有三个源任务的子网会转移到两个以上的其他任务。然而,如果我们允许转移性能下降2.5个百分点,那么七个源任务转移到至少一半的其他任务。
MLM任务生成传输性能最好的子网。
Q2:在子网可转移性中是否存在模式?
可转移性似乎与任务训练实例的数量有关。MRPC和WNLI的训练集最小;MRPC子网只传输到另一个任务,而WNLI子网不传输到任何其他任务。另一方面,MNLI和SQuAD拥有最大的培训集,由此产生的子网分别转移到四个和三个其他任务。MLM,这是迄今为止最大的培训集,也生产的子网络转移最好。有趣的是,我们没有看到任何证据表明迁移与任务类型相关(使用表1中描述的分组)。
Q3: 初始化为θ0是否会导致更好的转移?
在几乎所有的情况下,复卷对目标任务的传输性能都具有相同或更高的性能,而标准剪枝对传输性能的不利影响也很小。这表明,至少对SQuAD来说,在源任务上训练的重量似乎能提高而不是降低转会表现。
简短总结
本文提出之前的彩票假说在NLP和CV得到了广泛的验证,但是没有人做BERT这样的预训练模型的。于是作者提出了一种实验方式,在BERT上进行中奖彩票假说的验证,对各种任务都使用IMP的方法找到了子网,对此结果也做了很多子网模型和迁移学习方面的讨论和探究。
创新点
优劣
- 作者自问自答的模式讨论了很多内容,附加很完善的实验结果,比较全面,有理有据。
流程与公式
主要实验
8 - Pruning Pretrained Encoders with a Multitask Objective
论文内容
摘要
在这项工作中,我们在微调过程中对模型进行剪枝,以探讨是否有可能对单个编码器进行剪枝,从而使其可以用于多个任务。
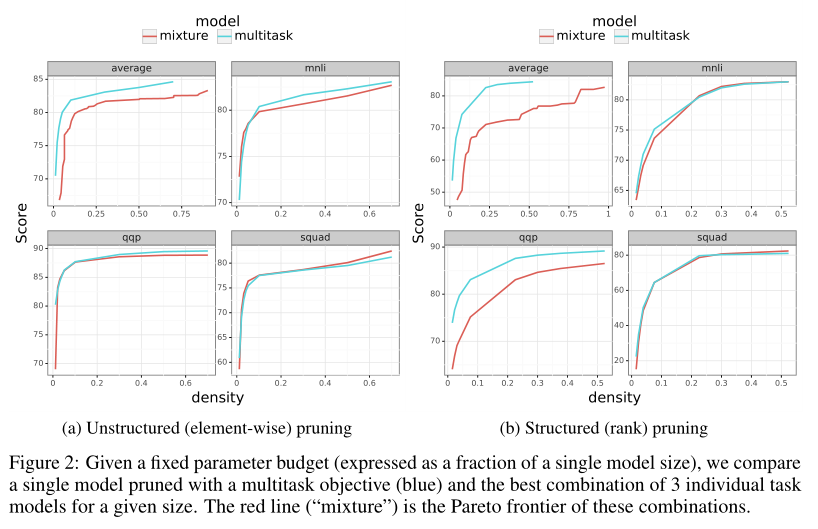
我们分配了一个固定的参数预算,并比较了多任务目标模型用于执行单任务与最佳的单任务模型之间的剪枝。我们发现,在两种剪枝策略下(元素剪枝(element pruning)和秩剪枝(rank pruning)),多任务目标的方法在所有任务结果平均时优于单任务模型,并且在每个任务上都表现不错。
在剪枝过程中使用多任务目标也可以有效地减少低资源任务(low-resource tasks)的模型大小。
4 结论
我们研究了多任务剪枝,其目的是在给定参数预算小于单任务模型的情况下,在多任务模型上表现良好。 通过对非结构化(element-wise)剪枝和结构化(rank)剪枝策略的研究,我们发现基于多任务目标的剪枝策略优于基于单个任务目标的多个剪枝模型组合的剪枝策略。 此外,我们发现具有多任务目标的剪枝(不需要额外的超参数调优)可以帮助进一步剪枝低资源数据集的任务。
1 引言
在这项工作中,我们探索了进一步减少这些多任务模型使用的参数数量,使其大大小于n的可能性。具体来说,我们的目标是通过使用一个多任务训练目标来修剪多任务模型。除了以上所述的优点之外,我们的目标是实现两个方面的最佳效果:一个经过大幅精简的模型,它在多个任务上也能很好地执行。
贡献
- 我们将结构化和非结构化剪枝方法扩展到多任务设置。
- 在这两种方法下,我们发现在给定的预算下,多任务模型始终优于单任务模型的组合。
- 使用多任务目标并不一定会导致任何单个任务的性能损失,在某些情况下,可以改进单个任务目标。
- 多任务目标能够提高具有较小数据集的任务的性能。
2 方法
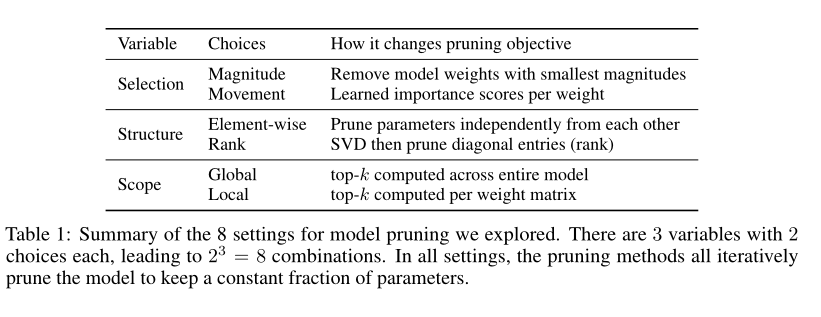
量化vs运动剪枝。我们探索了8种模型剪枝的设置,不同的剪枝方法(幅度vs.移动),被剪枝的内容(基于元素的(非结构化)剪枝vs.等级的(结构化)剪枝),以及在哪里(全局vs.局部)。表1总结了不同之处。我们使用稀疏性这个术语来指代被删除(或归零)的权重的比例。
2.2 多任务
将这些方法扩展到多任务设置是很简单的。我们为每个任务训练独立的、未修剪的分类头,同时在所有任务中共享一组修剪后的编码器权重(在运动修剪的情况下,还学习了重要性分数)。
3 实验和结构
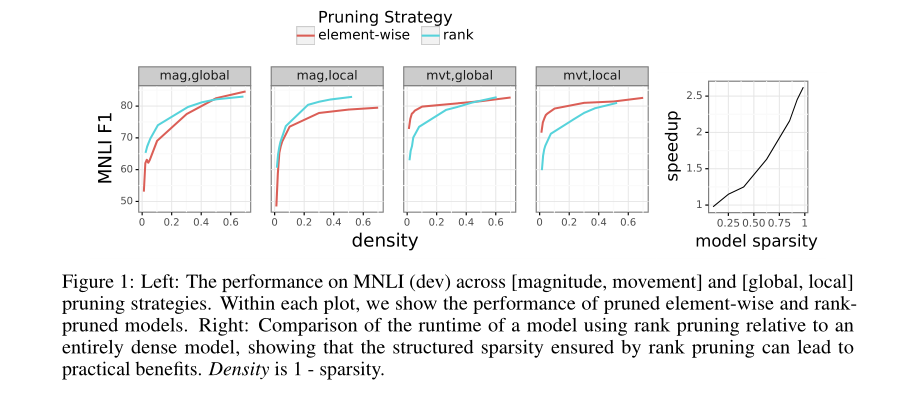
首先,我们在单个数据集上对这8种剪枝方法进行基准测试(第3.1节)。 目标是确定任务和实际的权衡之间的结构化和非结构化修剪和最佳设置。
在第3.2节中,我们将一个带有多任务目标的模型与单任务模型的集合进行比较,以探讨多任务目标是否有效。
最后,我们问,即使在单任务设置中,多任务目标是否可以作为辅助目标提供好处(章节3.3)。
3.1 比较修剪策略
各方法不同剪枝程度下的性能比较。
3.2 多任务修剪
具体来说,我们使用四个独立的目标:MNLI、QQP、SQuAD和multitask,将模型修剪到不同的稀疏程度。我们比较了单任务模型与多任务目标修剪后的单任务模型的最佳混合最好的混合是由Pareto frontier确定的。
可能的模型集合。图2显示了多任务模型在宏观平均3个任务指标上优于混合模型。此外,它匹配或超过单个任务的性能。我们发现,多任务剪枝优于混合元素剪枝和秩剪枝,这表明在剪枝过程中利用多任务目标的能力可以扩展到其他新的剪枝方法。这也证明,在编码器中,存在可以跨多个任务利用的较小的共享子网。
3.3 多任务训练作为辅助修剪目标
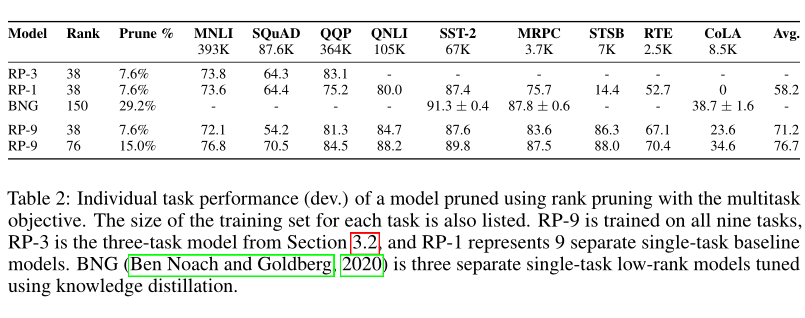
表2显示了使用局部大小秩剪枝时每个任务的性能。 这些结果表明,基于多任务的剪枝方法为低资源任务提供了一种有效剪枝模型的方法,而无需广泛的超参数搜索。
简短总结
本文使用多任务目标函数进行预训练的语言模型BERT的剪枝,使用了多种剪枝的方法,得出的结论是多任务模型的剪枝比单任务的效果都要好。也研究了多任务函数作为一种辅助函数去剪枝单任务目标的表现。
创新点
优劣
流程与公式
主要实验
9-Layer-wise Model Pruning based on Mutual Information
论文内容
摘要
受支持向量机(SVM)中基于互信息(mutual information, MI)的特征选择和逻辑回归的启发,本文提出了基于互信息的分层剪枝:对于多层神经网络的每一层,每次保留MI值相对上层神经元较高的神经元。从顶部的softmax层开始,从上往下逐层剪枝,直到到达底部的词嵌入层(word embedding layer)。
与基于权重的剪枝技术相比,本文提出的剪枝策略具有以下优点:(1)由于表示和矩阵可以压缩成更小但更密集的对应对象,从而避免了不规则的内存访问(irregular meory access),从而提高了速度;(2)基于顶层的训练信号,自上而下从更全局的角度进行剪枝,通过层层传播全局信号的效果来对每一层进行剪枝,在相同的稀疏级别上具有更好的性能。大量实验表明,在相同的稀疏程度下,该策略比基于权值的剪枝方法(如量化剪枝、运动剪枝)具有更好的速度和性能。
6 结论
本文提出了基于MI的自然语言处理模型剪枝方法。该模型避免了不规则的内存访问问题,在相同的稀疏程度下具有较高的速度。此外,该策略基于全局训练信号,采用自上而下的方式对模型进行裁剪,从而获得更高的准确率。在未来的工作中,我们应该放弃神经元值来自高斯分布的强烈假设。
1 引言
基于权值的方法已成功地应用于广泛的神经模型中进行模型剪枝,但存在以下缺点:(1)矩阵中的权值被不规则地剪枝,导致内存访问不规则,导致运行效率低下;(2)权矩阵的修剪是独立的,忽略了顶层训练信号的全局监督,忽略了连续层之间的信息传播,可能导致修剪后的网络的次优性。
本文受支持向量机中基于互信息(MI)的特征选择和逻辑回归的启发,提出了基于MI的分层剪枝方法,以解决上述NLP中基于权值的剪枝方法的缺点。
对于多层神经网络的每一层,相对于上层保存的神经元,MI值较高的神经元被保存。从顶部的softmax层开始,逐层剪枝,直到以自上而下的方式到达底部的输入字嵌入层。
贡献
本文解决了基于权值的剪枝的两个缺点:
(1)由于将剪枝后的表示和矩阵压缩成更小但更密集的表示和矩阵,避免了不规则的内存访问;与基于权重的剪枝方法相比,在相同的稀疏级别上,这能够显著加快计算速度;
(2)该方法不是根据每个权值单独查看每个权值矩阵,而是基于顶层的训练信号,从更全局的角度进行操作,将全局训练信号的效果自上而下地传播到连续的层中,对每一层进行修剪。这将在相同的稀疏级别上带来更好的性能。
3 模型
使用MI计算第1 - 1层和第l层维度之间的相关得分I(A, B)的定量方法。

互信息(MI)是两个随机变量之间量化信息量的一种度量,通过另一个变量得到关于一个变量的信息。MI的公式如下:
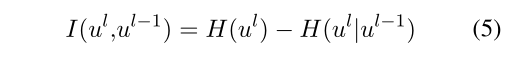
4 实验结果
将提出的策略与以下权值的剪枝模型进行比较:量化剪枝、运动剪枝、L0剪枝。
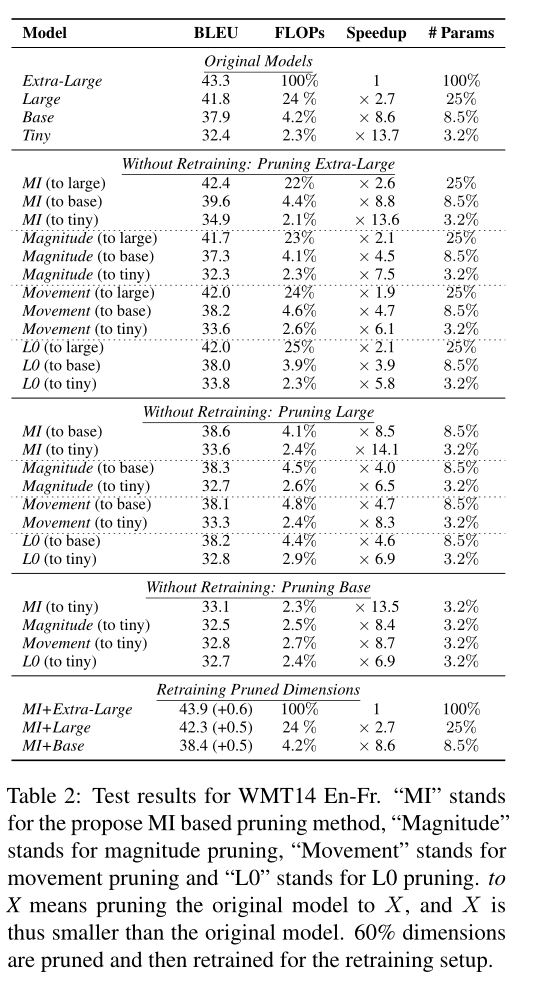
因为互信息策略提供了一种基于输出标签的更全局的特征(维度)选择策略,而不是在矩阵操作中关注局部矩阵权值。对于量级剪枝和运动剪枝,我们发现运动剪枝在较低的稀疏级别上表现较差,但在较高的稀疏级别上表现较好。
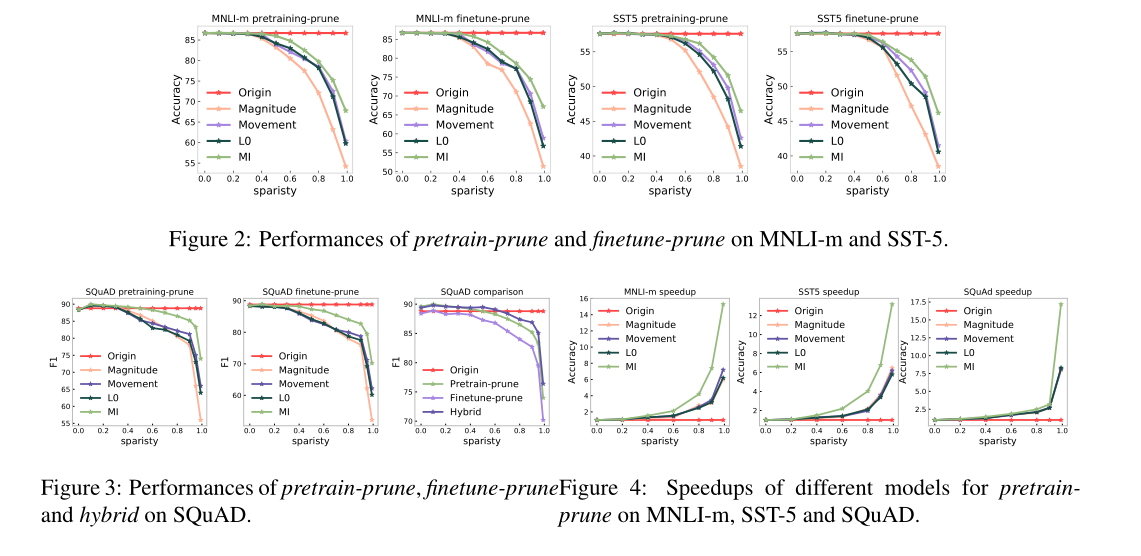
简短总结
使用互信息进行剪枝,和之前的基于剪枝的方法不同。解决的问题是:能避免不规则的内存访问,避免稀疏的操作,从而提高运行速度;能在剪枝的过程中看到更全局的信息,一层一层传递下来。
创新点
优劣
流程与公式
主要实验
10-Block Pruning For Faster Transformers
论文内容
摘要
剪枝方法是减小模型尺寸的有效方法,而知识蒸馏是加速推理的有效方法。
我们提出了一种针对小模型和快速模型的块剪枝(block pruning)方法。我们的方法通过考虑任意大小的块来扩展结构化方法,并将这种结构加到运动剪枝(movement pruning)中,然后进行微调。我们发现,这种方法学会了删除底层模型的完整组件,例如注意头。实验包含分类和生成任务,得到了一个剪枝后的模型,比其他模型快2.4倍,让在SQuADv1上构建的BERT变小了74%,在F1上只下降了1%,而且速度比知识蒸馏模型快,大小比剪枝模型小。
1 引言
结果
在这项工作中,我们的目标是通过块剪枝来缩小这一差距。与修剪单个参数不同,这种方法鼓励在密集硬件上进行优化的修剪。与结构化方法中通常使用的基于行或列的剪枝相比,这是一种不那么严格的方法(McCarley, 2019),结构化方法很难有效地应用于变压器。
我们将这种方法与运动剪枝相结合(Sanh等人,2020年),这是一种在微调过程中对预训练模型进行剪枝的简单方法。最后的方法1几乎没有额外的超参数或训练要求。
尽管在训练过程中使用了子行正方形块,该方法学会了消除模型的全部组件,有效地降低了大量的注意头。这种效果允许模型实现加速,甚至超过标准的结构修剪的前馈层。结果显示,在SQuAD v1.1上加速2.4倍,F1下降1%,在QQP上加速2.3倍,F1下降1%。在CNN/DailyMail的所有ROUGE指标上,总结的实验也显示了1.39倍的加速,平均下降2点,解码器的权重减少3.5倍。
8 结论
我们已经证明,我们可以提取小的剪枝模型,它们在一个等效或比蒸馏网络更好。这种方法可以在微调期间完成,而不是在培训前。该方法不求助于数据增强或架构搜索等技术,它适用于各种任务和基本模型。随着更好、更大的模型以越来越快的速度发布,我们可以依靠一种简单而稳健的方法,在不牺牲精度的情况下,在特定任务上加快它们的速度,并在保持大部分原始模型精度的情况下,轻松地分发这些模型。
4 块剪枝的模型
在此工作中,我们将运动剪枝扩展到局部参数块上。具体来说,变压器中的每个矩阵被划分为固定大小的块。这种设置超越了对非结构化方法的任意修剪,其目标是鼓励数据局部性更接近效率所需要的东西。
在过去的工作中,这个模型经过了精馏的训练,以匹配教师模型的性能。与其他需要完全指定新模型结构的精馏方法不同,我们的方法只需要块的大小和形状,即模型中每个参数矩阵的(m0, n0)集合。如果块太大,则很难对其进行修剪,但如果块太小,则不支持有效推理。
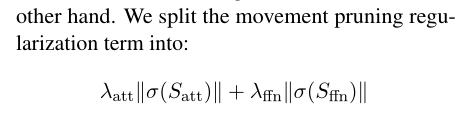

6 实验
图1显示了不同的块剪枝方法对注意层和前馈层的影响,蓝色被保留,粉色被修剪。我们发现,所有不同大小的块学会了在FFN层中修剪整个维度。有趣的是,我们发现block方法也可以从MHA中移除整个头部。

SQuAD的结果如图2所示,对于给定的速度,曲线越高,模型越精确。
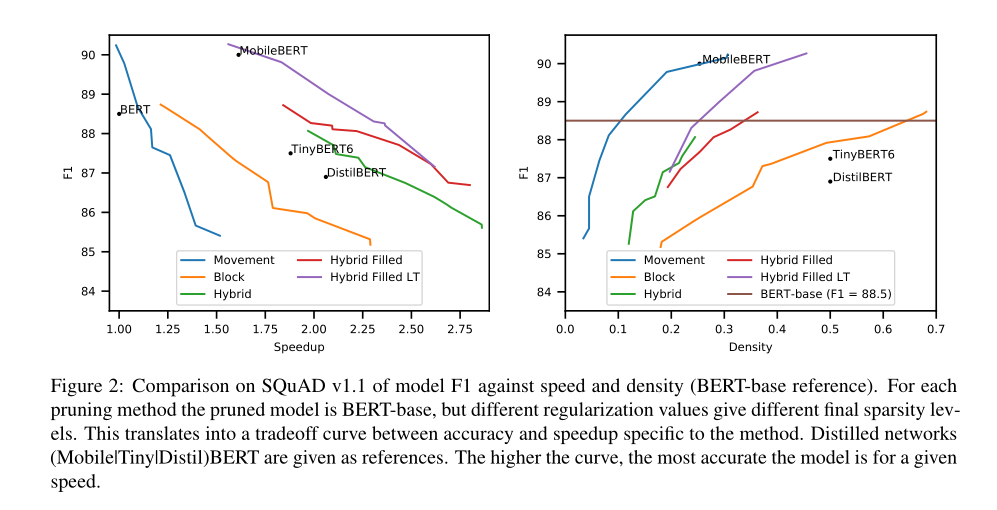
简短总结
创新点
优劣
流程与公式
主要实验
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
如果觉得文章内容不错,还请大力支持哦~
